Sage ima implementirane osnovne statističke funkcije, ali nama će biti zgodnije koristiti paket scipy.stats čije mogućnosti su trenutno veće.
sage: import scipy
sage: import scipy.stats
sage: import matplotlib.pyplot as plt
sage: import numpy as np
Kreirajmo prvo NumPy listu brojeva. NumPy liste imaju metode za izračun osnovnih statističkih veličina poput srednje vrijednosti, varijance, standardne devijacije itd.
sage: xs=np.linspace(1,9,21); xs
array([ 1. , 1.4, 1.8, 2.2, 2.6, 3. , 3.4, 3.8, 4.2, 4.6, 5. ,
5.4, 5.8, 6.2, 6.6, 7. , 7.4, 7.8, 8.2, 8.6, 9. ])
sage: print "%.2f +- %.2f" % (xs.mean(), xs.std())
5.00 +- 2.42
Obične liste nemaju gornje statističke metode pa ukoliko nas zanima npr. srednja vrijednost brojeva u običnoj listi treba je prvo konvertirati u numpy listu funkcijom np.array() ili možemo primijeniti Sage funkciju mean() (dakle ne metodu).
sage: mean([3, 5, 7, 9, 11])
7
scipy.stats paket ima implementirane brojne statističke raspodjele:
Svaka od tih raspodjela ima svoje parametre (npr. za Gaussovu raspodjelu su to srednja vrijednost i standardna devijacija). Oni se najčešće specificiraju putem opcionalnih argumenata, a točnu sintaksu saznajemo iz standardne dokumentacije.
Najvažnije metode distribucija su:
Tako je npr. vrijednost u \(x=0\) normalne distribucije sa srednjom vrijednosti \(\mu = 5\) i standardnom devijacijom \(\sigma = 1.5\), \(f(x=0, \mu=5, \sigma=1.5)\) dan s:
sage: scipy.stats.norm.pdf(0, loc=5., scale=1.5)
0.0010281859975274036
Skica distribucije i njenog integrala:
sage: xs = np.linspace(-2,12)
sage: fig, ax = plt.subplots(figsize=[5,3])
sage: ax.plot(xs, scipy.stats.norm.pdf(xs, loc=5., scale=1.5), label='pdf')
sage: ax.plot(xs, scipy.stats.norm.cdf(xs, loc=5., scale=1.5), 'r--',
....: label='cdf')
sage: ax.legend(loc='upper left').draw_frame(0)
sage: fig.savefig('fig')
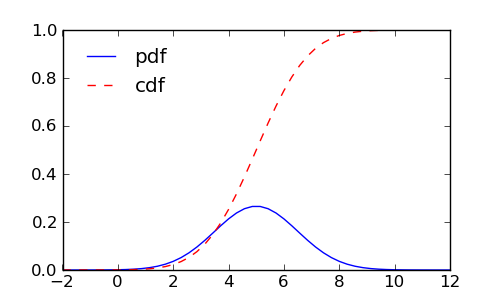
Izračunajmo vjerojatnost da se slučajna varijabla nađe unutar jedne standardne devijacije \(\sigma\) od srednje vrijednosti \(\mu\). Ona je dana integralom distribucije od \(\mu-\sigma\) do \(\mu+\sigma\). Kako na raspolaganju imamo funkciju cdf() koja daje integral od \(-\infty\) do \(x\), treba samo oduzeti dva takva integrala (koristimo i to da su defaultne vrijednosti loc=0 i scale=1):
sage: scipy.stats.norm.cdf(1) - scipy.stats.norm.cdf(-1)
0.68268949213708585
(To je čuvenih 68% vjerojatnosti.)
Zadatak 1
Slučajna varijabla \(X\) slijedi normalnu raspodjelu sa srednjom vrijednosti \(\mu=50\) i standardnom devijacijom \(\sigma=2\). Kolika je vjerojatnost da se \(X\) nađe između 47 i 54?
Sad ćemo metodom rvs() izgenerirati uzorak od 10000 brojeva raspodjeljenih po normalnoj raspodjeli s \(\mu=5\) i \(\sigma=1.5\) i testirati da su srednja vrijednost i standardna devijacija prema očekivanjima:
sage: pts=scipy.stats.norm.rvs(loc=5., scale=1.5, size=1e4)
sage: print "broj točaka = %i" % len(pts)
broj točaka = 10000
sage: print "srednja vrijednost = %.3f" % pts.mean() # rel tol 0.01
srednja vrijednost = 4.998
sage: print "standardna devijacija = %.3f" % pts.std() # rel tol 0.03
standardna devijacija = 1.493
Za crtanje histograma ovog uzorka koristimo Matplotlibovu hist() funkciju, čiji opcionalni argument bins kontrolira broj “binova” dakle broj intervala apscise u kojima se prebrojavaju točke:
sage: fig, ax = plt.subplots(figsize=[3.5,2])
sage: ax.hist(pts, bins=20, normed=True)
sage: fig.savefig('fig')
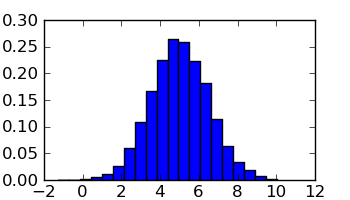
Ovo je bilo za jedan uzorak. Listu npr. standardnih devijacija za 5 nezavisnih uzoraka možemo konstruirati ovako:
sage: [scipy.stats.norm.rvs(loc=5, scale=1.5, size=1e4).std() for k in
....: range(5)] # rel tol 0.05
[1.503340173922008, 1.5040004762159596, 1.4785845284471362,
1.4906248759178866, 1.5136584591557063]
Zadatak 2
Kolika je vjerojatnost da mjerenje slučajne varijable koja slijedi normalnu razdiobu sa srednjom vrijednošću \(\mu\) i standardnom devijacijom \(\sigma\) odstupi od srednje vrijednosti za više od \(3\sigma\)?
Važna raspodjela je tzv. \(\chi^2\)-raspodjela
Vidimo da \(\chi^2\) raspodjela, pored argumenta x, ima samo jedan parametar: \(\nu\) = df = broj stupnjeva slobode (degrees of freedom) [1].
Srednja vrijednost \(\chi^2\) raspodjele jednaka je broju stupnjeva slobode:
sage: scipy.stats.chi2.rvs(3, size=1e5).mean() # rel tol 0.01
3.0033578764955071
Jedno od svojstava \(\chi^2\) raspodjele je da integral repa te raspodjele (s jednim stupnjem) od 1, 4, 9 do \(\infty\) daje vjerojatnost da mjerenje slučajne varijable raspodjeljene po Gaussovoj raspodjeli sa standardnom devijacijom \(\sigma\) odstupi od srednje vrijednosti za \(\sigma, 2\sigma, 3\sigma, \ldots\).
sage: [1-scipy.stats.chi2.cdf(eps^2,1) for eps in [1,2,3]]
[0.31731050786291404, 0.045500263896358528, 0.0026997960632602069]
Zadatak 3
Središnji granični teorem kaže da su srednje vrijednosti dovoljno velikih uzoraka neke raspodjele raspodjeljene prema normalnoj (Gaussovoj) raspodjeli bez obzira na to kakva je originalna raspodjela iz koje te uzorke uzimamo. U to ćemo se uvjeriti na primjeru \(\chi^2\) raspodjele.
Za ove iste primjere, ali izvedene pomoću Sage funkcija, vidi odjeljak Statistika - alternative.
Bilješke
| [1] | Naziv tog parametra postaje jasan u kontekstima određivanja dobrote prilagodbe i statističkog testiranja hipoteze. |