6. Još matematike

6.1. Kompleksna analiza

Matematičke funkcije se redovito ispravno ponašaju i za kompleksne vrijednosti argumenta

sage: log(-1+1e-8*I)
3.14159264358979*I
sage: log(-1-1e-8*I)
-3.14159264358979*I

Vidimo da logaritamska funkcija uredno radi s kompleksnim argumentom i daje nam glavnu granu multifunkcije s argumentom \(-\pi < arg(log(z)) \le \pi\), s diskontinuitetom od \(2\pi\) prilikom prelaska negativne realne osi.

sage: var('x, y')
(x, y)
sage: plot3d(imag(log(x+y*1j)), (x,-2,2), (y,-2,2))

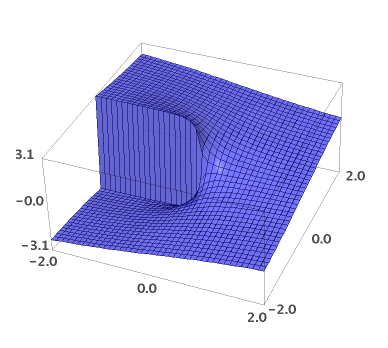
taylor() može dati i Laurentov razvoj u kompleksnoj ravnini. Npr, vrijedi

\[\frac{1}{z^2 + 1}=-\left(\frac{i}{2}\right)\frac{1}{z-i}-\left(\frac{i}{2}\right)^2-\left(\frac{i}{2}\right)^3(z-i)-\left(\frac{i}{2}\right)^4(z-i)^2-\cdots.\]

što do nultog reda dobivamo ovako:

sage: var('z')
z
sage: taylor(1/(z^2+1), z, I, 0)
-I/(2*z - 2*I) + 1/4

Za izračun reziduuma ne postoji posebna funkcija, ali i njega možemo dobiti pomoću funkcije taylor() zahvaljujući činjenici da je reziduum jednak minus prvom koeficijentu (onom uz \(1/(z-z_0)\)) u Laurentovom redu. Npr. tražimo reziduum funkcije \(f(z) = exp(z)/z^5\) u \(z=0\):

sage: lrnt = taylor(e^z/z^5, z, 0, -1); lrnt
1/24/z + 1/6/z^2 + 1/2/z^3 + 1/z^4 + 1/z^5

Možemo koristiti i formulu s limesom u polu:

sage: [limit(diff(z^k*e^z/z^5, z, k-1), z=0)/factorial(k-1) for k in
....:                                                       range(1,6)]
[+Infinity, -Infinity, +Infinity, -Infinity, 1/24]

Obje metode ispravno daju 1/24 za traženu vrijednost reziduuma.

Zadatak 1

Definirajte funkciju plotpoint(z) koja crta kompleksnu ravninu sa točkom koja odgovara kompleksnom broju z. Dakle x=Re(z), y=Im(z)

Zadatak 2

Definirajte funkciju argand(lista) koja crta kompleksnu ravninu s točkama zadanim u listi kompleksnih brojeva lista = [z1, z2, ...]. Upotrijebite je da nacrtate na jednom dijagramu svih devet devetih korijena od 1.

Zadatak 3

Definirajte funkciju plotfun(fun, min, max) koja crta realni i imaginarni dio funkcije fun za interval apscise (min, max).

6.2. Vektorska polja

Neka se čestica u ravnini nalazi u potencijalu \(U(x,y)= -4 x^2 y^3\). Odredimo odgovarajuću silu \({\bf F} = -{\bf \nabla} U\) To je moguće pomoću metode simboličkih izraza gradient() koja vraća odgovarajuće vektorsko polje sile:

sage: var('x y z')
(x, y, z)
sage: U = -4*x^2*y^3
sage: F = -U.gradient(); F
(8*x*y^3, 12*x^2*y^2)

Dakle, polje sile je \({\bf F} = 8 x y^3\, {\bf i} + 12 x^2 y^2\, {\bf j}\) i možemo ga skicirati funkcijom plot_vector_field():

sage: plot_vector_field(F, (x,-2,2), (y,-2,2))

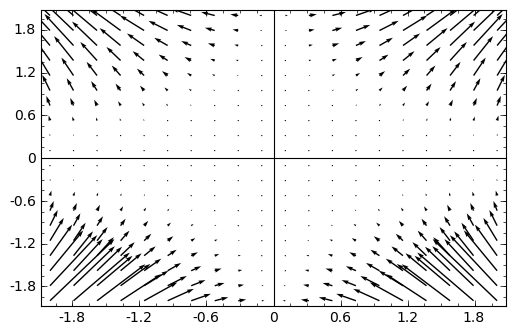
Ukoliko potencijal ovisi i o nekim parametrima moramo eksplicitno deklarirati varijable koordinatnog sustava. Isto trebamo i kad potencijal ne ovisi o nekoj koordinati. Npr. ukoliko je gornji potencijal zapravo \(U(x, y, z)\), dakle u 3D prostoru samo što ne ovisi o \(z\), onda imamo:

sage: F3 = -U.gradient([x,y,z]); F3
(8*x*y^3, 12*x^2*y^2, 0)

Sage nema specijalizirane funkcije za divergenciju i rotaciju, ali nije ih teško napisati. Jedan primjer nalazi se u datoteci dostupnoj ovako:

sage: load('http://www.phy.hr/~kkumer/sp/divcurl.py')
--- Loaded functions: div, curl

sage: div(F3, [x,y,z])
24*x^2*y + 8*y^3
sage: curl(F3, [x,y,z])
(0, 0, 0)

Provjerimo da je divergencija rotacije proizvoljne funkcije nula:

sage: div(curl([x^2 + 2*y, x^3 + sin(z), y*z + 2], [x,y,z]), [x,y,z])
0

Crtanje 3D vektorskog polja:

sage: plot_vector_field3d(F3, (x,-2,2), (y,-2,2), (z,-2,2))

6.3. Testiranje hipoteze

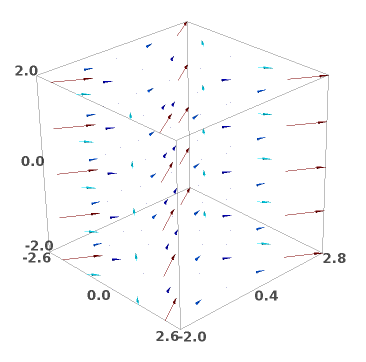
Često je potrebno kvantificirati dobrotu neke prilagodbe te odrediti da li predloženi teorijski model dobro opisuje mjerenja. Uzmimo slijedeći niz mjerenja s greškama \((x_i, y_i, \sigma_i\equiv\Delta y_i\)):

sage: errdata = [[0.55, 0.74, 0.20], [0.9, 1.07, 0.12],
....:      [1.2, 1.28, 0.12], [1.5, 1.02, 0.12], [1.9, 1.63, 0.20]]
sage: xs = [x for x,y,err in errdata]
sage: ys = [y for x,y,err in errdata]
sage: errs = [err for x,y,err in errdata]

Za crtanje točaka s greškama (errorbars), koristimo Matplotlib funkciju errorbar() gdje greške idu u opcionalni argument yerr:

sage: import matplotlib.pyplot as plt
sage: import numpy as np
sage: fig, ax = plt.subplots(figsize=[5,3])

sage: ax.errorbar(xs, ys, yerr=errs, linestyle='None')
sage: fig.savefig('fig')

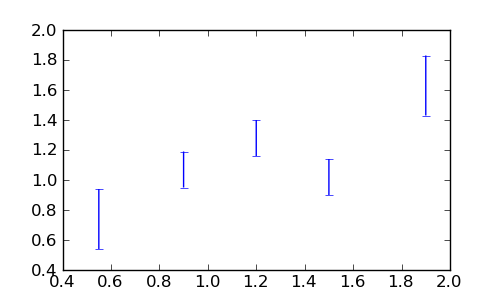
Promotrimo tri moguća teorijska opisa ovih mjerenja: potenciju \(x^a\), logaritam \(\log(a x)\) i obični pravac \(a + b x\) i odredimo parametre prilagodbom pomoću funkcije find_fit(). (Zasad zanemarimo različite greške pojedinih mjerenja.)

sage: var('a, b')
(a, b)
sage: powmodel(x) = x^a
sage: logmodel(x) = log(a*x)
sage: linmodel(x) = a*x+b

sage: powfit=find_fit([[x, y] for x,y,err in errdata], powmodel,
....:                             solution_dict=True); print powfit
{a: 0.6166290268412898}
sage: logfit=find_fit([[x, y] for x,y,err in errdata], logmodel,
....:                             solution_dict=True); print logfit
{a: 2.836898540272243}
sage: linfit=find_fit([[x, y] for x,y,err in errdata], linmodel,
....:                                   solution_dict=True); linfit
{b: 0.49690475972372317, a: 0.5380952396683008}

sage: xvals = np.linspace(0.4, 2)
sage: ax.plot(xvals, [powmodel(x).subs(powfit).n() for x in xvals],'r')
sage: ax.plot(xvals, [logmodel(x).subs(logfit).n() for x in xvals],'b-.')
sage: ax.plot(xvals, [linmodel(x).subs(linfit).n() for x in xvals],
....:                                   color='black', linestyle=':')
sage: fig.savefig('fig')

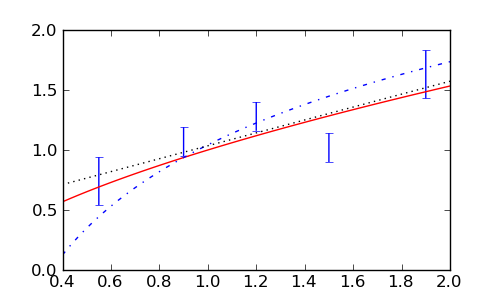
Teško je “od oka” procijeniti koji je opis najbolji, a još teže koji opisi su prihvatljivi a koji nisu. Standardna mjera dobrote fita je

\[\chi^2 = \sum_i \frac{(y_i - f(x_i))^2}{\sigma_{i}^2}\]

gdje su \(\sigma_i\) greške mjerenja. (Usput, kad je riječ o mjerenju frekvencija onda je greška dana kao \(\sigma_i=\sqrt{y_i}\).). Dobre su prilagodbe s \(\chi^2 \approx df\), gdje je \(df\) broj stupnjeva slobode (broj mjerenja minus broj slobodnih parametara funkcije koju prilagođavamo). Za točnije kvantificiranje dobrote prilagodbe gleda se integral statističke \(\chi^2\) raspodjele s \(df\) stupnjeva slobode od izračunatog \(\chi^2\) do beskonačnosti koji se često zove \(p\)-vrijednost i koji ne bi trebao biti manji od 0.1 ili barem 0.01 ili hipotezu treba odbaciti. Taj integral je implementiran kao funkcija scipy.stats.chisqprob(chisq, df). (Inače, za razliku od ovog primjera gdje tražimo statističku podršku hipotezi da funkcije opisuju mjerenja, često smo u obrnutoj situaciji gdje testiramo tzv. nul-hipotezu. Tu se npr. pitamo koja je vjerojatnost nekih mjerenja ukoliko neka čestica ne postoji ili ukoliko neki neki lijek ne djeljuje. Tada je mala p-vrijednost “poželjna” jer predstavlja statističku podršku postojanju te čestice ili dobrom djelovanju lijeka.)

Definirajmo tri funkcije koje prilagođavamo ...

sage: def powfun(p, x):
....:     return x^p[0]
....:
sage: def logfun(p, x):
....:     return log(p[0]*x)
....:
sage: def linfun(p, x):
....:     return p[1]*x+p[0]

... i odgovarajuću funkciju udaljenosti tj. odstupanja (čije kvadrate će minimizirati leastsq()). Tu trebamo staviti i težinski faktor \(1/\sigma_i\) za svaku točku kako bi točke s manjom greškom više utjecale na prilagodbu. Ovdje ćemo dodati još jedan argument putem kojeg ćemo prosljeđivati jednu od gornje tri funkcije:

sage: def dist(p, fun, data):
....:     return np.array([(y - fun(p, x))/err for (x,y,err) in data])

Definirajmo i odgovarajući \(\chi^2\):

sage: def chisq(p, fun, data):
....:     return sum( dist(p, fun, data)^2 )

Nakon minimizacije ćemo testirati i zastavicu ier tako da ukoliko leastsq() nije uspješna dobijemo odgovarajuću poruku o grešci:

sage: import scipy
sage: import scipy.stats
sage: fitfun = powfun
sage: ppow_final, cov_x, infodict, msg, ier = scipy.optimize.minpack.leastsq(
....:                dist, [1.],  (fitfun, errdata), full_output=True)
sage: if ier not in (1,2,3,4):
....:     print " -----> No fit! <--------"
....:     print msg
....: else:
....:     print "a =%8.4f +- %.4f" % (ppow_final, sqrt(cov_x[0,0]))
....:     chi2 = chisq([ppow_final], fitfun, errdata)
....:     df = len(errdata)-1
....:     print "chi^2 = %.3f" % chi2
....:     print "df = %i" % df
....:     print "p-vrijednost =  %.4f" % scipy.stats.chisqprob(chi2, df)
a =  0.5055 +- 0.1486
chi^2 = 7.880
df = 4
p-vrijednost =  0.0961

sage: fitfun = logfun
sage: plog_final, cov_x, infodict, msg, ier = scipy.optimize.minpack.leastsq(
....:               dist, [1.],  (fitfun, errdata), full_output=True)
sage: if ier not in (1,2,3,4):
....:     print " -----> No fit! <--------"
....:     print msg
....: else:
....:     print "a =%8.4f +- %.4f" % (plog_final, sqrt(cov_x[0,0]))
....:     chi2 = chisq([plog_final], fitfun, errdata)
....:     df = len(errdata)-1
....:     print "chi^2 = %.3f" % chi2
....:     print "df = %i" % df
....:     print "p-vrijednost =  %.4f" % scipy.stats.chisqprob(chi2, df)
a =  2.7219 +- 0.1693
chi^2 = 15.973
df = 4
p-vrijednost =  0.0031

sage: fitfun = linfun
sage: plin_final, cov_x, infodict, msg, ier = scipy.optimize.minpack.leastsq(
....:          dist, [1., 1.],  (fitfun, errdata), full_output=True)
sage: if ier not in (1,2,3,4):
....:     print " -----> No fit! <--------"
....:     print msg
....: else:
....:     parerrs = sqrt(scipy.diagonal(cov_x))
....:     print "p[0] =%8.3f +- %.4f" % (plin_final[0], parerrs[0])
....:     print "p[1] =%8.3f +- %.4f" % (plin_final[1], parerrs[1])
....:     chi2 = chisq(plin_final, fitfun, errdata)
....:     df = len(errdata)-2    # dva parametra
....:     print "chi^2 = %.3f" % chi2
....:     print "df = %i" % df
....:     print "p-vrijednost =  %.4f" % scipy.stats.chisqprob(chi2, df)
p[0] =   0.656 +- 0.2121
p[1] =   0.398 +- 0.1683
chi^2 = 7.116
df = 3
p-vrijednost =  0.0683

sage: fig, ax = plt.subplots(figsize=[5,3])
sage: ax.errorbar(xs, ys, yerr=errs, linestyle='None')
sage: xvals = np.linspace(0.4, 2)
sage: ax.plot(xvals, [powfun([ppow_final], x) for x in xvals],'r')
sage: ax.plot(xvals, [logfun([plog_final], x) for x in xvals],'b-.')
sage: ax.plot(xvals, [linfun(plin_final, x) for x in xvals], color='black',
....:             linestyle=':')
sage: fig.savefig('fig')

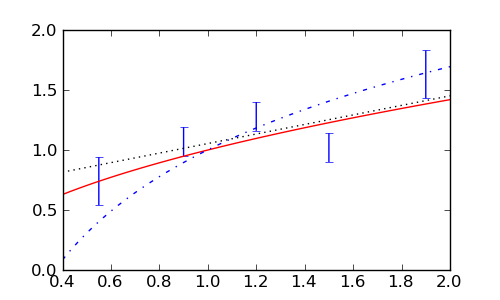
Ova analiza sugerira da možemo odbaciti logaritamski model, dok su druga dva modela, u nedostaku boljih, prihvatljiva.

Zadatak 4

Prilagodite funkciju \(f(x) = a x\) donjim podacima. Odredite parametar \(a\) i njegovu grešku te ocijenite dobrotu fita.

sage: xs2, ys2, errs2 = [range(2,25,2), [5.3,14.4,20.7,30.1,35.0,41.3,52.7,
....:                 55.7,63.0,72.1,80.5,87.9], [1.5 for k in range(2,25,2)]]
sage: errdata2 = zip(xs2, ys2, errs2)