4.7. Prilagodba funkcije podacima

Često je potrebno neke podatke dobivene npr. mjerenjima grafički prikazati i približno opisati nekom funkcijom (tzv. prilagodba ili “fitanje”).

sage: data = [[0.2,  0.1], [0.35,  0.2], [1, 0.6], [1.8, 0.9], [2.5, 1.3],
....:                                                   [4, 2.06], [5, 2.6]]

::

sage: list_plot(data, figsize=[3,3])

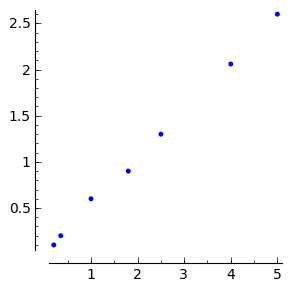
Klasična situacija je potreba za prilagodbom pravca \(f(x) = a + b x\) metodom najmanjih kvadrata (linearna regresija). Pogledajmo prvo kako bismo sami implementirali standardne formule za metodu najmanjih kvadrata:

sage: xs = [x for x,y in data]
sage: ys = [y for x,y in data]
sage: xs2 = [x^2 for x,y in data]
sage: ys2 = [y^2 for x,y in data]
sage: xys = [x*y for x,y in data]
sage: n = len(data)
sage: delc = n*sum(xs2) - sum(xs)^2
sage: b = (n*sum(xys)-sum(xs)*sum(ys))/delc
sage: a = (sum(xs2)*sum(ys)-sum(xs)*sum(xys))/delc
sage: sigsq = sum([(y-b*x-a)^2 for x,y in data])/(n-2)
sage: erra = sqrt(sum(xs2)*sigsq/delc)
sage: errb = sqrt(n*sigsq/delc)
sage: print "a = %.3f +- %.3f" % (a, erra)
a = 0.020 +- 0.023
sage: print "b = %.3f +- %.3f" % (b, errb)
b = 0.513 +- 0.008

Sage sadrži funkciju find_fit() koja radi otprilike to isto, ali je općenitija u smislu da krivulja koju prilagođavamo može biti zadana bilo kojim matematičkim izrazom. Pogledajmo prvo prilagodbu pravca:

sage: var('a b')
(a, b)
sage: model(x) = a + b*x

sage: fit = find_fit(data, model, solution_dict=True); fit
{b: 0.5130561168359806, a: 0.020159524186939004}

Ovdje smo zatražili ispis rješenja u obliku rječnika kako bismo ga lako uvrstili u model putem metode subs():

sage: list_plot(data, figsize=[3,3]) + plot(model(x).subs(fit), (x, 0, 5),
....:                                                           color='red')

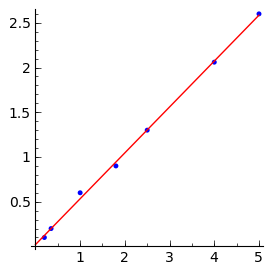
Zadatak 1

Donjim podacima iz liste data2 prilagodite polinom trećeg reda, te funkciju \(f(x)=a \sin(x)\) te nacrtajte sve na jednom grafu. Radi lakšeg snalaženja neka krivulje budu različitih boja. Izračunajte zbroj kvadrata odstupanja \(\sum_i (y_i - f(x_i))^2\) za oba slučaja.

sage: data2 = [[0, 0.1], [0.3, 0.4], [1, 0.7], [1.8, 1], [2.5, 0.5],
....:                                              [4, -0.6], [5, -1.0]]

Nažalost, find_fit() ne daje greške parametara pravca \(a\) i \(b\). Za to trebamo koristiti naprednije funkcije za prilagodbu. Zgodna takva funkcija je leastsq() iz paketa scipy.optimize. Ona kao svoj prvi argument traži funkciju koju minimiziramo (kod metode najmanjih kvadrata to je odstupanje funkcije u točki od ordinate točke, \(y_i - f(x_i)\), ali ne kvadrirano jer leastsq() sam radi kvadriranje!). Tu funkciju treba definirati kao Python funkciju. Npr. za prilagodbu pravca funkcija koju minimiziramo treba vraćati listu odstupanja pravca od točaka:

sage: def distances(p, data):
....:     return [(y - p[0] - p[1]*x) for x,y in data]

Prvi argument ove funkcije je lista p[] parametara koje prilagođavamo. Početne vrijednosti tih parametara specificiraju se u drugom argumentu funkcije``leastsq()``.

Treći argument* leastsq() je tuple s eventualnim dodatnim argumentima funkcije koju minimiziramo (prvi argument te funkcije je uvijek lista parametara koje prilagođavamo). Ovdje ćemo taj dodatni argument iskoristiti da proslijedimo toj funkciji same podatke (data) na koje prilagođujemo funkciju.

Po defaultu, leastsq() isto vraća samo tupl s listom prilagođenih vrijednosti parametara (bez grešaka) i zastavicom (flag) koja označava tip pronađenog rješenja ili eventualne probleme:

sage: import scipy
sage: scipy.optimize.leastsq(distances, [1.,1.],  (data,))
(array([ 0.02015952,  0.51305612]), 3)

Ukoliko želimo i greške koristimo opcionalni argument full_output=True, koji nam daje i tzv. matricu kovarijanci (cov_x dolje) iz koje odredimo greške parametara na slijedeći način [1].

sage: p_final, cov_x, infodict, msg, ier = scipy.optimize.leastsq(
....:                          distances, [1.,1.],  (data,), full_output=True)
sage: vr = scipy.dot(distances(p_final, data), distances(
....:                                p_final, data))/(len(data)-len(p_final))
sage: p_errs = sqrt(scipy.diagonal(vr*cov_x))
sage: print "p[0] =%8.3f +- %.4f" % (p_final[0], p_errs[0])
p[0] =   0.020 +- 0.0231
sage: print "p[1] =%8.3f +- %.4f" % (p_final[1], p_errs[1])
p[1] =   0.513 +- 0.0085

leastsq() također omogućuje i prilagodbu složenijih funkcija. Npr. možemo se pitati trebamo li gornjoj funkciji dodati i kvadratni član:

sage: def distances(p, data):
....:     return [(y - p[0] - p[1]*x - p[2]*x^2) for x,y in data]

sage: p_final, cov_x, infodict, msg, ier = scipy.optimize.leastsq(
....:                    distances, [1.,1.,1.],  (data,), full_output=True)
sage: vr = scipy.dot(distances(p_final, data), distances(p_final,
....:                                 data))/(len(data)-len(p_final))
sage: p_errs = sqrt(scipy.diagonal(vr*cov_x))
sage: for k in range(len(p_final)):
....:     print "p[%i] =%8.3f +- %.4f" % (k, p_final[k], p_errs[k])
p[0] =   0.027 +- 0.0350
p[1] =   0.502 +- 0.0373
p[2] =   0.002 +- 0.0071

Činjenica da je greška paramera p[2] znatno veća od vrijednosti samog parametra, sugerira da je kvadratni član suvišan. (Štoviše, vidimo da je i slobodni član p[0] od malog značaja.)

Bilješke

[1]

Gornji način određivanja greške parametara se može prihvatiti kao recept, no za one koji žele znati evo objašnjenja: Kad se minimizira ispravno normalizirana funkcija onda dijagonalni elementi matrice kovarijanci izravno daju greške parametara. No, za običnu prilagodbu metodom najmanjih kvadrata, minimizira se kvadrat apsolutne greške pa je potrebno renormalizirati matricu kovarijanci varijancom mjerenja, a procjenitelj te varijance je upravo var=(suma kvadrata odstupanja)/(broj stupnjeva slobode). Inače, kad se tako vrijednost kvadrata odstupanja iskoristi za procjenu greške mjerenja ista se više ne može jednostavno iskoristiti za procjenu dobrote fita. (Vidi diskusiju u Bevingtonu ispod Eq. (6.15).)