8. Alternative

Kako je Sage nastao združivanjem velikog broja već ranije postojećih matematičkih rutina, mnogi računi se mogu izvesti na više načina. U ovom poglavlju je ponovno izloženo nešto materijala iz poglavlja Matematika, ali s alternativnim izborom rutina.

8.1. Linearna algebra (alternativa)

U ovom odjeljku radimo iste stvari kao u odjeljku Linearna algebra, ali koristeći “domaće” funkcije Sagea, a ne NumPy modul.

Vektori i matrice se konstruiraju pomoću funkcija vector() i matrix() kojima kao argument dajemo listu elemenata, odnosno, u slučaju matrice, listu listi elemenata (listu redak-vektora)

sage: vec1 = vector([1,1,2])
sage: vec2 = vector((2,2,4))    # može i tupl

Množenje vektora skalarom je prirodno:

sage: 3*vec1
(3, 3, 6)

Skalarni produkt vektora se može ostvariti putem dot_product() metode vektora,

sage: vec1.dot_product(vec2)
12

ali i kao obično množenje:

sage: vec1*vec2
12

Vektorski produkt ide samo putem metode cross_product() (nema zapisa s \(\times\)!):

sage: vec1.cross_product(vec2)
(0, 0, 0)

Norma (“duljina”) vektora:

sage: vec2.norm()
2*sqrt(6)

Množenje matrica te množenje matrice i vektora ide na prirodan način:

sage: mat = matrix([[1, 2, 1], [4, 3, 3], [9, 1, 7]]); mat
[1 2 1]
[4 3 3]
[9 1 7]

sage: mat*mat
[18  9 14]
[43 20 34]
[76 28 61]

sage: mat*vec1
(5, 13, 24)

Inverz matrice se može ostvariti putem metode inverse(), potenciranjem na minus-prvu potenciju ili operatorom ~:

sage: ~mat
[-18/7  13/7  -3/7]
[  1/7   2/7  -1/7]
[ 23/7 -17/7   5/7]

sage: ~mat*mat    # provjera
[1 0 0]
[0 1 0]
[0 0 1]

sage: mat2 = matrix([[1., 2.], [3., 4.]])
sage: mat2
[1.00000000000000 2.00000000000000]
[3.00000000000000 4.00000000000000]

Defaultno polje realnih brojeva nad kojim su definirane matrice u Sageu nije sasvim pogodno za numeričke račune pa je pogodno matrice s realnim koeficijentima kreirati uz eksplicitnu deklaraciju polja RDF (“real double field”):

sage: mat2 = matrix(RDF, [[1., 2.], [3., 4.]])
sage: mat2
[1.0 2.0]
[3.0 4.0]

Pristup pojedinim elementima matrice se isto izvodi indeksiranjem:

sage: mat[0, 0] = 0; mat
[0 2 1]
[4 3 3]
[9 1 7]

Zadatak 1

Za datu matricu A definiramo svojstvene vektore (eigenvectors) \({\bf v}\) i njima pripadajuće svojstvene vrijednosti \(\lambda\) (eigenvalues) kao rješenja matrične jednadžbe

\[A {\bf v} = \lambda {\bf v}\;.\]

Odredite svojstvene vrijednosti i svojstvene vektore matrice

\[\begin{split}\left(\begin{array}{cc} 2.3 & 4.5 \\ 6.7 &-1.2 \end{array}\right) \;,\end{split}\]

i provjerite da dobivena rješenja zaista zadovoljavaju gornju jednadžbu.

Zadatak 2

Kreirajte 3x3 matricu sa slučajnim realnim brojevima između 0 i 10. Invertirajte je i pomnožite s originalnom matricom te se uvjerite da dobijete jediničnu matricu.

Elementi vektora i matrica mogu biti i simboli:

sage: var('x y z')
(x, y, z)

sage: vec3 = vector([x, y, z])
sage: vec3.norm()
sqrt(x*conjugate(x) + y*conjugate(y) + z*conjugate(z))

Dijagonalizacija matrice \(A\) je pronalaženje njenog rastava oblika

\[A = P D P^{-1}\]

gdje je \(D\) dijagonalna matrica. To se izvodi metodom eigenmatrix_right() koja vraća matrice \(P\) i \(D\):

sage: A = matrix(QQ, [[3, 1], [1, 3]])  # is_diagonalizable ne radi nad ZZ
sage: print A.is_diagonalizable()
True
sage: D, P = A.eigenmatrix_right(); (D, P)
(
[4 0]  [ 1  1]
[0 2], [ 1 -1]
)

sage: A == P*D*(~P) # provjera
True

Treba uočiti da su elementi dijagonalne matrice \(D\) i stupci matrice \(P\) upravo svojstvene vrijednosti odnosno svojstveni vektori od \(A\).

sage: A.eigenvectors_right()
[(4, [
(1, 1)
], 1), (2, [
(1, -1)
], 1)]

Neke matrice nisu dijagonalizabilne, u slučaju čega će matrice \(P\) i \(D\) koje vraća eigenmatrix_right() i dalje zadovoljavati

\[AP = PD\]

ali \(P\) neće biti invertibilna:

sage: A = matrix(QQ, [[1, 1], [0, 1]])
sage: print A.is_diagonalizable()
False
sage: D, P = A.eigenmatrix_right(); (D, P)
(
[1 0]  [1 0]
[0 1], [0 0]
)

sage: A*P == P*D
True

sage: ~P
Traceback (most recent call last):
...
ZeroDivisionError: input matrix must be nonsingular

U slučajevima kad matricu nije moguće dijagonalizirati od koristi može biti i vrlo popularni rastav na singularne vrijednosti (singular value decomposition, SVD):

\[A = U S V^{\dagger}\]

gdje su \(U\) i \(V\) unitarne, a \(S\) dijagonalna matrica. (Jedino treba imati na umu da je odgovarajuća metoda SVD() trenutno implementirana samo za matrice nad realnim RDF poljem pa je po potrebi potrebno prvo provesti konverziju matrice.)

sage: U, S, V = matrix(RDF, A).SVD()

sage: U*S*V.conjugate_transpose()
[                  1.0    1.0000000000000002]
[9.443400922348744e-17                   1.0]

Zadatak 3

Stupci matrice \(U\) u SVD rastavu su svojstveni vektori matrice \(A A^\dagger\), a odgovarajuće svojstvene vrijednosti su kvadrati elemenata dijagonale matrice \(S\). Uvjerite se u to eksplicitno na gornjem primjeru.

Svi vektori iste vrste i dimenzije su elementi apstraktnog vektorskog prostora koji je dostupan putem metode parent():

sage: vec1 = vector([1,1,2])
sage: vecspace=vec1.parent(); vecspace
Ambient free module of rank 3 over the principal ideal domain Integer Ring

Ovdje je važno uočiti da je je prostor definiran na prstenu cijelih brojeva. Naravno, vektori mogu biti i nad drugim prstenovima/poljima:

sage: print vector([1/3, 1/4]).parent()
Vector space of dimension 2 over Rational Field
sage: vector([1., 2.]).parent()
Vector space of dimension 2 over Real Field with 53 bits of precision

Baza vektorskog prostora:

sage: vecspace.basis()
[
(1, 0, 0),
(0, 1, 0),
(0, 0, 1)
]

Matrice isto imaju svoje apstraktne prostore kojima pripadaju:

sage: print mat.parent()
Full MatrixSpace of 3 by 3 dense matrices over Integer Ring
sage: (~mat).parent()
Full MatrixSpace of 3 by 3 dense matrices over Rational Field

sage: mat2 = matrix([[1., 2.], [3., 4.]])
sage: mat2.parent()
Full MatrixSpace of 2 by 2 dense matrices over Real Field with 53 bits of precision
sage: mat2
[1.00000000000000 2.00000000000000]
[3.00000000000000 4.00000000000000]

Ukoliko pokušamo već stvorenom vektoru nad poljem nekih brojeva zamijeniti neki element simbolom, to ne ide:

sage: vec1[2] = x
Traceback (most recent call last):
...
TypeError: unable to convert x to an integer

Riječ je o tome da su npr. čisto realni vektori (nad poljem RDF) interno reprezentirani kao C-polja radi optimizacije. Da bismo mogli napraviti ovo što želimo trebamo prvo konvertirati vektor u simbolički vektor. Tu konverziju radi odgovarajući vektorski prostor nad simboličkim prstenom (SR, symbolic ring). Taj prostor dobijemo pomoću metode parent() vektora istog ranga, ali koji već jest simbolički. (Za detalje o takvim konverzijama vidi prvih par odjeljaka ovdje.)

sage: vec3.parent()
Vector space of dimension 3 over Symbolic Ring

sage: vec1_symb = vec3.parent()(vec1)  # konverzija vec1 u simbolicki vektor

sage: vec1_symb[1] = x; vec1_symb    # sad ide
(1, x, 2)

8.2. Diferencijalne jednadžbe (alternativa)

Alternativna rutina za numeričko rješavanje diferencijalnih jednadžbi je Sageov ode_solver(). Slično kao i za SciPyjev odeint() problem treba organizirati kao sustav diferencijalnih jednadžbi prvog reda oblika

\[\frac{d y_i}{dt} = f_i(y, t) \quad i=1, 2, \ldots \;,\]

te je potrebno definirati funkciju koja vraća listu \([f_0(t), f_1(t), \ldots]\), gdje je dopuštena i dodatna ovisnost o nekim konstantnim parametrima sustava. Npr. za van der Polovu jednadžbu takva funkcija se može definirati ovako:

sage: def syst(t, y, params):
....:     return [y[1], params[0]*(1 - y[0]^2)*y[1] - y[0]]

Sučelje za ode_solver() je više u stilu objektno-orjentiranog programiranja: ta funkcija kreira ode_solver objekt i sve ostalo se izvodi putem metoda tog objekta. Prilikom kreiranja možemo zadati sustav jednadžbi (definiran gornjom funkcijom).

sage: S = ode_solver(syst)

Metoda ode_solver objekta koja integrira diferencijalne jednadžbe je ode_solve(), čiji važni argumenti su početni uvjeti y_0 = \([y_{0}(0), y_{1}(0), \ldots ]\), vremenski interval evolucije sustava t_span = \([t_0, t_{\rm max}]\) i broj točaka integracije num_points, a ukoliko sustav ovisi i o nekim parametrima specificiramo ih opcijom params:

sage: S.ode_solve(y_0 = [1,0], t_span=[0,15], params=[3], num_points=150)

Rješenje je kao i u slučaju rješavanja funkcijom odeint lista točaka (u malo drugačijem formatu), a postoji i funkcija interpolate_solution() koja interpolira te točke i pretvara ih u funkciju. Opcionalni argument te funkcije i, određuje koju od funkcija \(y_i(t)\) želimo:

sage: S.solution[:3]
[(0, [1, 0]), (0.1, [0.9950026686448377, -0.09990818686134167]),
(0.2, [0.9800189364740901, -0.19985749159625474])]

sage: xt = S.interpolate_solution(i=0)
sage: yt = S.interpolate_solution(i=1)

sage: plot(xt, (0,15)) + plot(yt, (0,15), color='red')

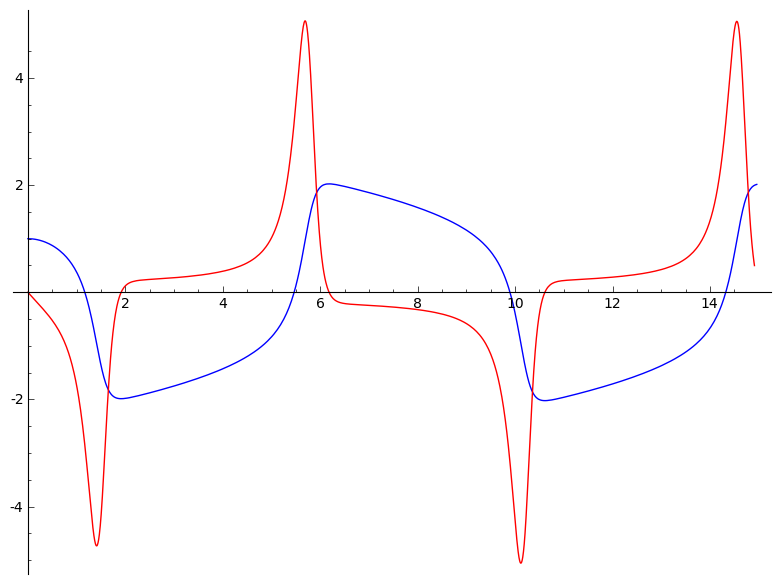
Jedna zanimljiva prednost ode_solver pristupa je da omogućuje da se izvrijednjavanje funkcija koje stoje s desne strane diferencijalnih jednadžbi preseli iz Pythona u C, pomoću tzv. cythona:

sage: %cython
sage: cimport sage.gsl.ode
sage: import sage.gsl.ode
sage: include 'gsl.pxi'
sage: cdef class van_der_pol(sage.gsl.ode.ode_system):
....:     cdef int c_f(self,double t, double *y,double *dydt):
....:         dydt[0]=y[1]
....:         dydt[1]=(1 - y[0]*y[0])*y[1] - y[0]
....:         return GSL_SUCCESS
....:     cdef int c_j(self, double t,double *y,double *dfdy,double *dfdt):
....:         dfdy[0]=0
....:         dfdy[1]=1.0
....:         dfdy[2]=-2.0*y[0]*y[1]-1.0
....:         dfdy[3]=(1 - y[0]*y[0])
....:         dfdt[0]=0
....:         dfdt[1]=0
....:         return GSL_SUCCESS

Ovdje smo osim funkcija \(f_i(y, t)\) koje definiraju sustav, definirali i jakobijan \(df_i/dy_j\).

sage: T = ode_solver()
sage: T.algorithm = "bsimp"
sage: vander = van_der_pol()
sage: T.function=vander

Za sustav iz ovog odjeljka ubrzanje je samo četverostruko, ali taj faktor može biti i osjetno veći za kompliciranije jednadžbe.

sage: %time
sage: S.ode_solve(y_0 = [1,0], t_span=[0,150], params=[1], num_points=1e5)
CPU time: 10.18 s,  Wall time: 10.65 s

sage: %time
sage: T.ode_solve(y_0 = [1,0], t_span=[0,150], num_points=1e5)
CPU time: 2.20 s,  Wall time: 2.20 s

Još jednu alternativu za numeričko integriranje diferencijalnih jednažbi nudi “domaća” Sageova funkcija desolve_system_rk4().

8.3. Statistika (alternativa)

U ovom odjeljku ćemo, bez puno komentara, napraviti identične primjere kao u odjeljku Statistika, ali koristeći isključivo “domaće” Sage funkcije, a ne SciPy i NumPy.

sage: xs =[ 1. ,  1.4,  1.8,  2.2,  2.6,  3. ,  3.4,  3.8,  4.2,  4.6,  5. ,
....:           5.4,  5.8,  6.2,  6.6,  7. ,  7.4,  7.8,  8.2,  8.6,  9. ]

sage: print "srednja vrijednost = %.1f" % mean(xs)
srednja vrijednost = 5.0
sage: print "varijanca = %.3f" % variance(xs,
....:       bias=True)  # default bias=False dijeli s 1/(len(xs)-1)
varijanca = 5.867
sage: print "standardna devijacija = %.3f" % std(xs, bias=True)
standardna devijacija = 2.422

sage: G = RealDistribution('gaussian', 1.5)
sage: G.distribution_function(-5)
0.0010281859975274036

sage: G.plot((-7, 7), figsize=[3.5,2])

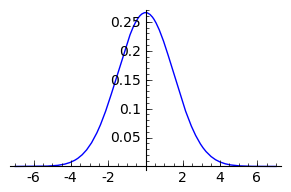
sage: G.cum_distribution_function(1.5)-G.cum_distribution_function(-1.5)
0.6826894921370859

sage: pts = [5 + G.get_random_element() for k in range(1e4)]
sage: print "broj točaka = %i" % len(pts)
broj točaka = 10000
sage: print "srednja vrijednost = %.1f" % mean(pts)  # rel tol 0.02
srednja vrijednost = 5.0
sage: print "standardna devijacija = %.3f" % std(pts) # rel tol 0.02
standardna devijacija = 1.497

sage: G.generate_histogram_plot('fig', num_samples=1e4, bins=20)

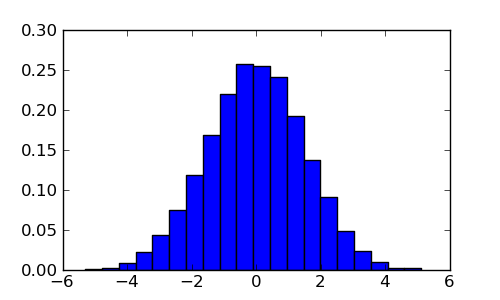
sage: [mean([5 + G.get_random_element() for k            # abs tol 0.05
....:         in range(10000)]) for k in range(5)]
[4.98977720776, 5.00428769154, 5.00979362618, 4.9901576697, 4.99635335439]

sage: CHISQ = RealDistribution('chisquared', 3)
sage: mean([CHISQ.get_random_element() for k in range(1000)])  # rel tol 0.1
3.032640511

sage: CHISQ = RealDistribution('chisquared', 1)
sage: [1-CHISQ.cum_distribution_function(eps^2) for eps in [1,2,3]]
[0.3173105078629148, 0.04550026389635842, 0.002699796063260207]

8.4. Prilagodba funkcije podacima (alternativa)

Alternativna mogućnost za prilagodbu funkcije podacima je poznati specijalizirani jezik za statističku analizu R, koji je sadržan u Sage distribuciji (premda je sučelje još uvijek relativno primitivno). Linearna regresija pomoću R-sučelja ide ovako:

sage: data = [[0.2,  0.1], [0.35,  0.2], [1, 0.6], [1.8, 0.9],
....:                                   [2.5, 1.3], [4, 2.06], [5, 2.6]]
sage: rx = r([x for x,y in data])
sage: ry = r([y for x,y in data])
sage: r.summary(r.lm(ry.tilde(rx)))

Call:
lm(formula = sage16)

Residuals:
         1          2          3          4          5          6          7
-0.0227707  0.0002708  0.0667844 -0.0436605 -0.0027998 -0.0123840  0.0145599

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.020160   0.023057   0.874    0.422
sage7       0.513056   0.008488  60.446 2.35e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0381 on 5 degrees of freedom
Multiple R-squared: 0.9986, Adjusted R-squared: 0.9984
F-statistic:  3654 on 1 and 5 DF,  p-value: 2.345e-08

Ovdje gore dobivamo prvo residuals, što su odstupanja prilagođene funkcije od pojedinih točaka, zatim coefficients, što su parametri pravca gdje imamo i statistički test signifikantnosti parametara (zadnji stupac Pr(>|t|) gdje je manja brojka bolja). Na kraju, zadnji broj (p-value) označava dobrotu prilagodbe određenu putem tzv F-testa, gdje je prilagodba dobra ukoliko je p-value manji od 0.01 ili barem 0.1.

Usput, određivanje gore navedenih p-vrijednosti za parametre ide ovako:

sage: import scipy.stats
sage: print 2*(1-scipy.stats.t.cdf(0.02016/0.023057, 5))
0.42192862901
sage: 2*(1-scipy.stats.t.cdf(0.513056/0.008488, 5))
2.3454928665955777e-08