

Next: About this document ...
Up: Collectivity of the low-lying
Previous: Conclusions
- 1
- F. E. Bertrand, Nucl. Phys. A 354 (1981) 129c.
- 2
- F. Dawson and R. J. Furnstahl, Phys. Rev. C 42 (1990)
2009.
- 3
- D. Vretenar, A. Wandelt, and P. Ring,
to be published in Phys. Lett. B (2000).
- 4
- Y. K. Gambhir, P. Ring, and A. Thimet,
Ann. Phys. NY. 198 (1990) 132.
- 5
- M. L`Huillier and N. Van Giai,
Phys. Rev. C 39 (1989) 2022.
- 6
- P. Ring, Progr. Part. Nucl. Phys. 37 (1996) 193.
- 7
- D. Vretenar, H. Berghammer, and P. Ring,
Nucl. Phys. A581 (1995) 679.
- 8
- D. Vretenar, N. Paar, P. Ring and G. A. Lalazissis,
Phys. Rev. E 60 (1999) 308.
- 9
- G. A. Lalazissis, D. Vretenar, and P. Ring,
Nucl. Phys. A4516 (1999) 1.
- 10
- G. A. Lalazissis, D. Vretenar, and P. Ring,
Phys. Rev. C 57 (1998) 2294.
- 11
- F. Catara, C. H. Dasso, and A. Vitturi,
Nucl. Phys. A602 (1996) 181.
- 12
- Y. Suzuki, K. Ikeda, and H. Sato,
Prog. Theor. Phys. 83 (1990) 180.
- 13
- R. Mohan, M. Danos and L. C. Biedenharn,
Phys. Rev. C 5 (1971) 1740.
- 14
- D. Vretenar, N. Paar, P. Ring, and G. A. Lalazissis,
submitted to Phys. Lett. B (2000).
- 15
- T. Aumann et al.,
Nucl. Phys. A 649 (1999) 297c.
- 16
- M. Zinser et al.,
Nucl. Phys. A 619 (1997) 151.
- 17
- T. Nakamura et al.,
Phys. Lett. B 331 (1994) 296.
- 18
- T. Hartmann, J. Enders, P. Mohr, K. Vogt, S. Volz, and
A. Zilges, Phys. Rev. Lett. 85 (2000) 274.
- 19
- J. P. Adams, B. Castel and H. Sagawa,
Phys. Rev. C 53 (1996) 1016.
- 20
- J. Chambers, E. Zaremba, J. P. Adams and B. Castel,
Phys. Rev. C 50 (1994) R2671.
- 21
- H. Sagawa and T. Suzuki,
Phys. Rev. C 59 (1999) 59.
- 22
- Z. W. Bell, L. S. Cardman and P. Axel,
Phys. Rev. C 25 (1982) 791.
- 23
- G. Kühner, D. Meuer, S. Müller, A. Richter, E. Spamer,
O. Titze and W. Knüpfer,
Phys. Lett. B 104 (1981) 189.
- 24
- F. Catara, E. G. Lanza, M. A. Nagarajan and A. Vitturi,
Nuc. Phys. A 624 (1997) 449.
- 25
- H. Sagawa, N. Van Giai, N. Takigawa, M. Ishihara and
K. Yazaki, Z. Phys. A 351 (1995) 385.
- 26
- H. Sagawa and C. A. Bertulani,
Prog. Theor. Phys.(sup.) 124 (1996) 143.
- 27
- S. Ottini-Hustache, et. al.,
Phys. Rev. C 59 (1999) 3429.
- 28
- Z. Y. Ma, N. Van Giai, A. Wandelt, D. Vretenar and
P. Ring, nucl-th/9910054.
- 29
- F. E. Serr, T. S. Dumitrescu, T. Suzuki and C. H. Dasso,
Nucl. Phys. A 404 (1983) 359.
Figure Captions
- Fig.1 Isovector dipole strength in
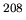 Pb
for the full RRPA(solid line) and RRPA without
contributions from Dirac states (dashed). The dotted, dot-dashed and
short-dashed lines correspond to the RRPA with only
Pb
for the full RRPA(solid line) and RRPA without
contributions from Dirac states (dashed). The dotted, dot-dashed and
short-dashed lines correspond to the RRPA with only 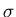 ,
, 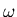 and
and
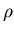 mesons included in the antiparticle-hole couplings, respectively.
mesons included in the antiparticle-hole couplings, respectively.
- Fig.2 Isovector dipole strength calculated with RRPA for a sequence of
oxygen isotopes (Z=8, N=8,14,16,20). Low energy region is noted with dotted
line.
- Fig.3 Ratio of the energy weighted moment m
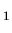 in the low (E
in the low (E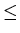 10 MeV)
and high (E
10 MeV)
and high (E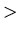 10 MeV) energy region for various nuclei.
10 MeV) energy region for various nuclei.
- Fig.4 Isovector (dotted line) and isoscalar (thick line)
dipole transition densities of
low-lying and GDR selected states in
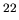 O and
O and 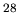 O.
Separated proton and neutron transition densities are displayed by
the dashed and dot-dashed lines, respectively. All transition densities are
multiplied by r
O.
Separated proton and neutron transition densities are displayed by
the dashed and dot-dashed lines, respectively. All transition densities are
multiplied by r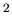 .
.
- Fig.5 Dipole strength for isovector mode of oscillations in the
 Ca,
Ca, 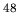 Ca,
Ca,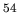 Ca and
Ca and 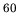 Ca nuclei.
Ca nuclei.
- Fig.6 Isovector (dotted line) and isoscalar (thick line)
dipole transition densities multiplied by r
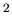 for the
low-lying (7.3 MeV) and GDR (15.2 MeV) state in
for the
low-lying (7.3 MeV) and GDR (15.2 MeV) state in 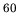 Ca.
Proton and neutron transition densities are displayed by
the dashed and dot-dashed lines, respectively.
Ca.
Proton and neutron transition densities are displayed by
the dashed and dot-dashed lines, respectively.
- Fig.7 Isovector dipole strength distributions for
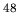 Ni,
Ni, 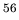 Ni,
Ni,
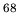 Ni and
Ni and 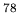 Ni nuclei.
Ni nuclei.
- Fig.8 Isovector (IV) and isoscalar (IS) dipole transition densities
multiplied by r
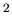 for the low-lying (8.9 MeV) and GDR (16.4 MeV) state in
for the low-lying (8.9 MeV) and GDR (16.4 MeV) state in
 Ni. Proton and neutron transition densities are noted
by p and n, respectively.
Ni. Proton and neutron transition densities are noted
by p and n, respectively.
- Fig.9 Centroid energies(
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) of the isovector dipole low-lying
(
) of the isovector dipole low-lying
(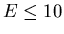 MeV) and GDR (
MeV) and GDR ( MeV) modes, displayed as a function of
number of neutrons in Ni isotopes.
Energies of the low-lying modes are compared with the hydrodynamical
prediction [12] for energy of the pygmy resonances (SIS).
GDR modes are compared with the mass dependence law
MeV) modes, displayed as a function of
number of neutrons in Ni isotopes.
Energies of the low-lying modes are compared with the hydrodynamical
prediction [12] for energy of the pygmy resonances (SIS).
GDR modes are compared with the mass dependence law 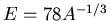 .
.
- Fig.10 Isovector dipole strength distributions for
 Sn,
Sn, 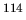 Sn,
Sn,
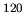 Sn and
Sn and  Sn nuclei.
Sn nuclei.
- Fig.11 Isovector (IV) and isoscalar (IS) dipole transition densities
multiplied by r
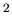 for low-lying 8.9 MeV (a) and GDR 14.8 MeV state (b)
in
for low-lying 8.9 MeV (a) and GDR 14.8 MeV state (b)
in  Sn. Proton and neutron transition densities are noted
by p and n, respectively. The contributions of the proton-neutron core
(Z=50,
Sn. Proton and neutron transition densities are noted
by p and n, respectively. The contributions of the proton-neutron core
(Z=50,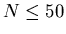 )(dashed) and the excess neutrons (
)(dashed) and the excess neutrons ( )(solid)
are displayed for the pygmy (c) and GDR (d) state.
)(solid)
are displayed for the pygmy (c) and GDR (d) state.
- Fig.12 Velocity distributions in
 Sn for the RRPA state at
8.6 MeV. The velocity field of the proton-neutron core (Z=50,
Sn for the RRPA state at
8.6 MeV. The velocity field of the proton-neutron core (Z=50,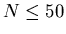 )(a)
is separated from the contribution of the excess neutrons (
)(a)
is separated from the contribution of the excess neutrons ( )(b).
)(b).
- Fig.13 The same as in Fig.12, but for the GDR peak at 14.8 MeV
in
 Sn.
Sn.
- Fig.14: Isovector low-lying (
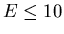 MeV) and GDR (
MeV) and GDR ( MeV)
energies as a function of neutron number in Sn isotopes.
Energies of the low-lying mode are compared with the hydrodynamical
prediction [12] of pygmy resonances (SIS). GDR modes are
compared with the mass dependence law
MeV)
energies as a function of neutron number in Sn isotopes.
Energies of the low-lying mode are compared with the hydrodynamical
prediction [12] of pygmy resonances (SIS). GDR modes are
compared with the mass dependence law 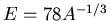 .
.
- Fig.15 Isovector dipole strength distribution in
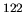 Zr (a).
The neutron(n), proton(p), isovector(IV) and isoscalar(IS)
transition densities are displayed for the low-lying state 7.7 MeV (b).
Separated transition densities of
the excess neutrons
Zr (a).
The neutron(n), proton(p), isovector(IV) and isoscalar(IS)
transition densities are displayed for the low-lying state 7.7 MeV (b).
Separated transition densities of
the excess neutrons 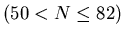 vibrating against the core (Z=40, N=50)
are shown in the (c) panel.
vibrating against the core (Z=40, N=50)
are shown in the (c) panel.
- Fig.16 Velocity distributions in
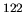 Zr for the low-lying RRPA
state at
7.7 MeV. The velocity field of the proton-neutron core (Z=40,
Zr for the low-lying RRPA
state at
7.7 MeV. The velocity field of the proton-neutron core (Z=40,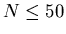 )(a)
is separated from the contribution of the excess neutrons (
)(a)
is separated from the contribution of the excess neutrons ( )(b).
)(b).
Table:
Dominant neutron particle-hole excitations for
the main peaks in low energy region of isovector
dipole strength for 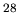 O.
O.
| E[MeV] |
EWSR[%] |
p-h excitation |
| 4.2 |
0.9 |
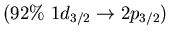 |
| 4.9 |
1.4 |
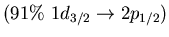 |
| |
|
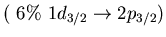 |
| 7.3 |
1.9 |
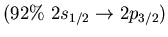 |
| 8.9 |
6.3 |
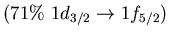 |
| |
|
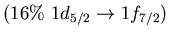 |
| |
|
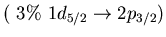 |
Table:
Neutron particle-hole excitations in the
low energy isovector dipole mode in 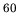 Ca.
Ca.
| E[MeV] |
EWSR[%] |
p-h excitation |
| 5.7 |
1.2 |
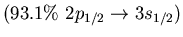 |
| |
|
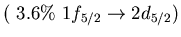 |
| 6.8 |
2.6 |
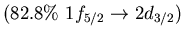 |
| |
|
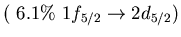 |
| |
|
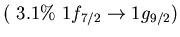 |
| |
|
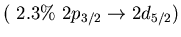 |
| |
|
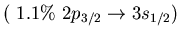 |
| 7.3 |
1.6 |
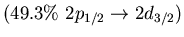 |
| |
|
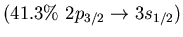 |
| |
|
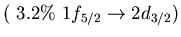 |
| |
|
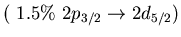 |
| 7.9 |
2.0 |
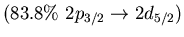 |
| |
|
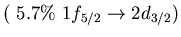 |
| |
|
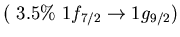 |
| |
|
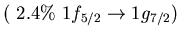 |
| 9.9 |
2.1 |
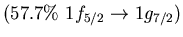 |
| |
|
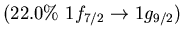 |
| |
|
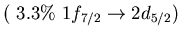 |
Table:
Main neutron particle-hole configurations
participating in the low-lying isovector dipole
state 9.0 MeV (4.3% EWSR) in 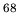 Ni (left) and 8.6 MeV state (1.4% EWSR)
in
Ni (left) and 8.6 MeV state (1.4% EWSR)
in  Sn(right)
Sn(right)
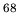 Ni, 9.0 MeV Ni, 9.0 MeV |
 Sn, 8.6 MeV Sn, 8.6 MeV |
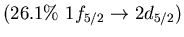 |
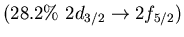 |
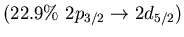 |
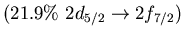 |
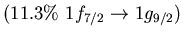 |
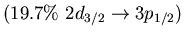 |
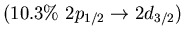 |
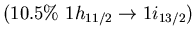 |
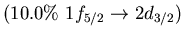 |
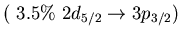 |
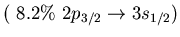 |
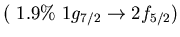 |
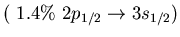 |
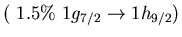 |
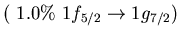 |
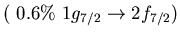 |
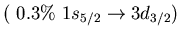 |
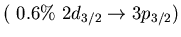 |


Next: About this document ...
Up: Collectivity of the low-lying
Previous: Conclusions
Nils Paar, 2001.

