The RRPA strength function (![]() ) for dipole excitation is
evaluated for several oxygen isotopes.
The calculations have been performed in the large configuration
space including both particle-hole pairs, and pairs formed from
hole states and negative-energy states. Discrete spectra is averaged with
the Lorentzian distribution,
) for dipole excitation is
evaluated for several oxygen isotopes.
The calculations have been performed in the large configuration
space including both particle-hole pairs, and pairs formed from
hole states and negative-energy states. Discrete spectra is averaged with
the Lorentzian distribution,
In Fig.2 we present the dipole strength distributions
(![]() ) for
) for ![]() O,
O, ![]() O,
O,![]() O and
O and ![]() O nuclei.
For
O nuclei.
For ![]() O the isovector
giant resonance is located at
O the isovector
giant resonance is located at ![]() =21.8 MeV. The adding of extra neutrons
leads to two interesting phenomena: a) increased fragmentation of dipole
strength, and b) appearance of the low lying dipole strength below 10 MeV.
The first appearance of the low energy peak below 10 MeV is
observed in
=21.8 MeV. The adding of extra neutrons
leads to two interesting phenomena: a) increased fragmentation of dipole
strength, and b) appearance of the low lying dipole strength below 10 MeV.
The first appearance of the low energy peak below 10 MeV is
observed in ![]() O. When moving further to the neutron drip line, the
contribution of the low energy (E
O. When moving further to the neutron drip line, the
contribution of the low energy (E![]() 10 MeV) strength increase relatively
more than the high energy response. This can be seen in corresponding
curve of Fig.3, where the ratio of separated energy
weighted moment m
10 MeV) strength increase relatively
more than the high energy response. This can be seen in corresponding
curve of Fig.3, where the ratio of separated energy
weighted moment m![]() from low (E
from low (E![]() 10 MeV) and high (E
10 MeV) and high (E![]() 10 MeV)
energy region is presented as a function of excess neutrons
10 MeV)
energy region is presented as a function of excess neutrons
![]() , with
, with ![]() .
In the Hartree-Fock plus random phase approximation, using Skyrme effective
interaction [24], in addition to the spreading of the
isovector dipole strength, several peaks are obtained for
.
In the Hartree-Fock plus random phase approximation, using Skyrme effective
interaction [24], in addition to the spreading of the
isovector dipole strength, several peaks are obtained for ![]() O in the
region 6-10 MeV, in contrast to the
O in the
region 6-10 MeV, in contrast to the ![]() O, with no low-energy
contributions. In the case of
O, with no low-energy
contributions. In the case of ![]() O the most collective RRPA peak
at 15.2 MeV exhausts 24% of EWSR, while in the non-relativistic RPA
approach [24] the most collective state exhausts approximately
15% of total EWSR.
Recent experimental investigation [15]
of giant resonances in
unstable oxygen isotopes
O the most collective RRPA peak
at 15.2 MeV exhausts 24% of EWSR, while in the non-relativistic RPA
approach [24] the most collective state exhausts approximately
15% of total EWSR.
Recent experimental investigation [15]
of giant resonances in
unstable oxygen isotopes ![]() O,
O,![]() O and
O and ![]() O shows the onset of
low-lying dipole strength, exhausting around 5% of the Thomas Reiche Kuhn
sum rule for energies up to 5 MeV above the continuum threshold. Further
experimental study involving the drip line nucleus
O shows the onset of
low-lying dipole strength, exhausting around 5% of the Thomas Reiche Kuhn
sum rule for energies up to 5 MeV above the continuum threshold. Further
experimental study involving the drip line nucleus ![]() O is expected in
the near future. In the framework of the relativistic random phase
approximation, we
observe 2.5%, 7.0% and 8.6% of the energy weighted sum rule (EWSR)
contributions from the
O is expected in
the near future. In the framework of the relativistic random phase
approximation, we
observe 2.5%, 7.0% and 8.6% of the energy weighted sum rule (EWSR)
contributions from the ![]() MeV peaks in
MeV peaks in ![]() O,
O,![]() O and
O and ![]() O
nuclei, respectively. In comparison, dipole strengths
below 15 MeV within the large scale shell model calculations exhaust
10% and 8.6% of the classical sum rule in
O
nuclei, respectively. In comparison, dipole strengths
below 15 MeV within the large scale shell model calculations exhaust
10% and 8.6% of the classical sum rule in ![]() O and
O and ![]() O,
respectively [21].
Let us investigate whether these soft
dipole modes are collective, as a consequence of the coherent superposition
of many single particle-hole configurations, like in the
giant resonances. The question whether the soft
excitation is collective or single-particle, have been already studied
in the light nuclei
O,
respectively [21].
Let us investigate whether these soft
dipole modes are collective, as a consequence of the coherent superposition
of many single particle-hole configurations, like in the
giant resonances. The question whether the soft
excitation is collective or single-particle, have been already studied
in the light nuclei ![]() Li and
Li and ![]() Be, concluding that the soft
mode of excitation is a new type of independent particle excitation,
characterized by a narrow width and a large transition strength, as a
consequence of the large spatial extension of the bound single-particle
states [25]. Within the RRPA investigation of oxygen isotopes,
we analyze in more details the main peaks contributing to the low-lying
isovector dipole strength. In order to estimate the role of each
particle-hole excitation, we separate contributions of
each proton and neutron p-h configuration by evaluating the fraction parameter
Be, concluding that the soft
mode of excitation is a new type of independent particle excitation,
characterized by a narrow width and a large transition strength, as a
consequence of the large spatial extension of the bound single-particle
states [25]. Within the RRPA investigation of oxygen isotopes,
we analyze in more details the main peaks contributing to the low-lying
isovector dipole strength. In order to estimate the role of each
particle-hole excitation, we separate contributions of
each proton and neutron p-h configuration by evaluating the fraction parameter
| (11) |
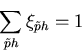 |
(12) |
Dominant low-energy peak in ![]() O which exhausts 2.5% of EWSR,
located at 9.3 MeV is mainly due to the neutron particle hole
excitations
O which exhausts 2.5% of EWSR,
located at 9.3 MeV is mainly due to the neutron particle hole
excitations
![]() and
and
![]() .
In the case of
.
In the case of ![]() O, three main peaks in the low-energy region appear:
6.9 MeV (3.1% EWSR), 7.4 MeV (1.6% EWSR) and 9.3 MeV (2.3% EWSR). They
correspond to the neutron excitations
O, three main peaks in the low-energy region appear:
6.9 MeV (3.1% EWSR), 7.4 MeV (1.6% EWSR) and 9.3 MeV (2.3% EWSR). They
correspond to the neutron excitations
![]() ,
,
![]() and
and
![]() ,
respectively, which reduce the role of other neutron and proton p-h
excitations. For extremely neutron rich nucleus
,
respectively, which reduce the role of other neutron and proton p-h
excitations. For extremely neutron rich nucleus ![]() O, larger
fragmentation is observed also in the low-energy region. We note here four
main low-energy peaks at 4.2 MeV, 4.9 MeV, 7.3 MeV and 8.9 MeV,
which are dominated again by the neutron excitations. Dominant particle-hole
configurations for low-lying excitations in
O, larger
fragmentation is observed also in the low-energy region. We note here four
main low-energy peaks at 4.2 MeV, 4.9 MeV, 7.3 MeV and 8.9 MeV,
which are dominated again by the neutron excitations. Dominant particle-hole
configurations for low-lying excitations in ![]() O are presented in the
Table
O are presented in the
Table ![]() . The main contribution in the low-energy
region comes from excitations of the excess neutrons in the 1d
. The main contribution in the low-energy
region comes from excitations of the excess neutrons in the 1d![]() ,
2s
,
2s![]() and 1d
and 1d![]() orbitals, but only one p-h excitation is relevant
in each low-energy peak, in contrast to large number of p-h excitations
contributing in the high-energy giant resonance. The transition densities
of characteristic low and high energy isovector dipole modes, are shown
in Fig.4 for
orbitals, but only one p-h excitation is relevant
in each low-energy peak, in contrast to large number of p-h excitations
contributing in the high-energy giant resonance. The transition densities
of characteristic low and high energy isovector dipole modes, are shown
in Fig.4 for ![]() O and
O and ![]() O nuclei. Here, we present the
proton and neutron transition densities, and the corresponding
isoscalar and isovector transition densities (solid line and dotted line,
respectively). According to Ref. [24], it is expected for the
isoscalar B(E1) to all states
to vanish, but if the neutron and proton transition densities have different
shapes, as is the case for the nuclei close to the drip line, the
corresponding isoscalar dipole transition density will be non-zero. Transition
densities for the main peak at 20.9 MeV and 18.1 MeV for
O nuclei. Here, we present the
proton and neutron transition densities, and the corresponding
isoscalar and isovector transition densities (solid line and dotted line,
respectively). According to Ref. [24], it is expected for the
isoscalar B(E1) to all states
to vanish, but if the neutron and proton transition densities have different
shapes, as is the case for the nuclei close to the drip line, the
corresponding isoscalar dipole transition density will be non-zero. Transition
densities for the main peak at 20.9 MeV and 18.1 MeV for ![]() O and
O and
![]() O display a radial dependence of isovector giant dipole resonance
(GDR), with protons and neutrons oscillating in opposite phases. Similar to
the study in the Hartree-Fock plus random phase approximation with Skyrme
forces [24],
the large neutron component in the surface region contributes to the
existence of a node in the isoscalar transition density, moving toward larger
value of radial coordinate, as the number of neutrons increase. Proton and
neutron transition densities of GDR peak have similar radial dependence at
large radii. Transition densities of selected low-energy peaks for
O display a radial dependence of isovector giant dipole resonance
(GDR), with protons and neutrons oscillating in opposite phases. Similar to
the study in the Hartree-Fock plus random phase approximation with Skyrme
forces [24],
the large neutron component in the surface region contributes to the
existence of a node in the isoscalar transition density, moving toward larger
value of radial coordinate, as the number of neutrons increase. Proton and
neutron transition densities of GDR peak have similar radial dependence at
large radii. Transition densities of selected low-energy peaks for
![]() O and
O and ![]() O show quite different behavior. The proton and neutron
densities in the interior region of both nuclei are not out of phase, and
the transition densities have characteristic long tail with almost no
contribution from the protons. Similar behavior of transition densities
have been observed in the neutron-rich light nuclei
O show quite different behavior. The proton and neutron
densities in the interior region of both nuclei are not out of phase, and
the transition densities have characteristic long tail with almost no
contribution from the protons. Similar behavior of transition densities
have been observed in the neutron-rich light nuclei ![]() He,
He, ![]() Li and
Li and
![]() Be where the large extended tails of the loosely-bound
neutron wave functions are responsible to cause different radial behavior
of the low-energy peaks when compared with those of giant
resonances [26].
Be where the large extended tails of the loosely-bound
neutron wave functions are responsible to cause different radial behavior
of the low-energy peaks when compared with those of giant
resonances [26].
Next we investigate the low-lying dipole excitations in
calcium isotopes. Isovector dipole strength distributions
for ![]() Ca,
Ca,![]() Ca,
Ca, ![]() Ca and
Ca and ![]() Ca nuclei are displayed
in Fig.5. As the neutron excess increase, the
fragmentation of the spectra is increased. In the case of
Ca nuclei are displayed
in Fig.5. As the neutron excess increase, the
fragmentation of the spectra is increased. In the case of
![]() Ca and
Ca and ![]() Ca no contribution for energies less than 10 MeV
is observed. The onset of low-lying dipole strength
is manifested after
Ca no contribution for energies less than 10 MeV
is observed. The onset of low-lying dipole strength
is manifested after ![]() Ca. This is in agreement with
the non-relativistic RPA calculations of Ref. [24].
It is also noted that the centroid energies move to
lower values with increasing neutron number in both models.
In addition,
no
Ca. This is in agreement with
the non-relativistic RPA calculations of Ref. [24].
It is also noted that the centroid energies move to
lower values with increasing neutron number in both models.
In addition,
no ![]() MeV contributions in
MeV contributions in ![]() Ca have been recognized
when compared with the
Ca have been recognized
when compared with the ![]() Ca.
In the RRPA investigation of extremely neutron rich nuclei
Ca.
In the RRPA investigation of extremely neutron rich nuclei ![]() Ca,
many peaks are contributing in the E
Ca,
many peaks are contributing in the E![]() 10 MeV region, together
exhausting 9.9% of the EWSR in contrast to the 39.4% EWSR of the main
GDR peak at 15.2 MeV. For the low-lying dipole strength, the most important
are excitations of neutrons from
orbitals 1f
10 MeV region, together
exhausting 9.9% of the EWSR in contrast to the 39.4% EWSR of the main
GDR peak at 15.2 MeV. For the low-lying dipole strength, the most important
are excitations of neutrons from
orbitals 1f![]() , 2p
, 2p![]() , 2p
, 2p![]() (
(![]() Ca) and 1f
Ca) and 1f![]() (
(![]() Ca) in the last shell. Dominant p-h
transitions in the highest low-energy
peaks for
Ca) in the last shell. Dominant p-h
transitions in the highest low-energy
peaks for ![]() Ca are listed in the Table
Ca are listed in the Table ![]() . In almost all
peaks, single particle-hole transition is dominant, only at 7.3 MeV
two comparable transitions have important role in the dipole transition
strength. The role of other allowed neutron and proton p-h excitations
is very small. Therefore the degree of collectivity in the low-energy region
of
. In almost all
peaks, single particle-hole transition is dominant, only at 7.3 MeV
two comparable transitions have important role in the dipole transition
strength. The role of other allowed neutron and proton p-h excitations
is very small. Therefore the degree of collectivity in the low-energy region
of ![]() Ca is very limited, single particle-hole nature of these modes
dominates. On the other side, GDR peak is characterized by a large number
of comparable p-h excitations, where the largest single neutron p-h
contribution is 20%, while the ratio of neutron and proton participation
61.8%/36.7%=1.7 is close to the ratio of neutron and proton
numbers. In contrast to the density functional theory calculations
[20], collective pygmy oscillations in calcium isotopes
have not been
observed in the RRPA investigation.
Ca is very limited, single particle-hole nature of these modes
dominates. On the other side, GDR peak is characterized by a large number
of comparable p-h excitations, where the largest single neutron p-h
contribution is 20%, while the ratio of neutron and proton participation
61.8%/36.7%=1.7 is close to the ratio of neutron and proton
numbers. In contrast to the density functional theory calculations
[20], collective pygmy oscillations in calcium isotopes
have not been
observed in the RRPA investigation.
Experimental results on low energy dipole strength in calcium isotopes
are still under debate. There was no evidence of low-lying mode
when comparing the
![]() Ca and
Ca and ![]() Ca in experiments with heavy ion reactions
[27]. On the other side, recent results [18] obtained
with the high resolution photon scattering experiments show concentration of
low-lying dipole strength in
Ca in experiments with heavy ion reactions
[27]. On the other side, recent results [18] obtained
with the high resolution photon scattering experiments show concentration of
low-lying dipole strength in ![]() Ca.
The sum B(E1) strength between 5
and 10 MeV is about 10 times larger than in
Ca.
The sum B(E1) strength between 5
and 10 MeV is about 10 times larger than in ![]() Ca.
Ca.
RRPA transition
densities for the case of selected low (7.3 MeV) and GDR (15.2 MeV) states
of ![]() Ca are displayed in the Fig.6. At the GDR energy,
proton and neutron densities oscillate in opposite phases, as it is expected
for an isovector resonance. Because of the very large neutron number,
the isoscalar transition density does not vanish, similar
to the non-relativistic approach [24]. In the
interior of the nucleus isoscalar transition density is comparable
with the isovector one.
However, its contribution decreases close to the surface region, where
it changes sign. On the
other side, the transition densities of low-energy peak show quite
opposite behavior, with a neutron dominated tail beyond the nuclear
surface region.
Ca are displayed in the Fig.6. At the GDR energy,
proton and neutron densities oscillate in opposite phases, as it is expected
for an isovector resonance. Because of the very large neutron number,
the isoscalar transition density does not vanish, similar
to the non-relativistic approach [24]. In the
interior of the nucleus isoscalar transition density is comparable
with the isovector one.
However, its contribution decreases close to the surface region, where
it changes sign. On the
other side, the transition densities of low-energy peak show quite
opposite behavior, with a neutron dominated tail beyond the nuclear
surface region.