Zračenje crnog tijela

Spektakularan primjer besmislenog rezultata klasične fizike je problem spektralne distribucije zračenja crnog tijela. To je ujedno i najmarkantniji primjer razrješenja problema zahvaljujući uvođenju Planckove kvantne hipoteze, već i zato što je tako dobivena prva kvantnomehanička formula uopće - naime Planckov zakon zračenja (1.17).

Najbolji emiter zračenja je ono tijelo koje je najbolji apsorber - to je jednostavan rezultat ravnotežne termodinamike. Idealni apsorber se u fizičarskom žargonu naziva ``crno tijelo", a jedna jednostavna realizacija koja izvrsno aproksimira takav idealni apsorber - pa prema tome i idealni emiter - je maleni otvor na inače zatvorenoj, iznutra začađenoj šupljini. Postavimo to u veliku pećnicu koju držimo na stalnoj temperaturi T, i pričekamo da začađena šupljina dođe s njom u toplinsku ravnotežu. Tada je i elektomagnetsko zračenje unutar šupljine u termičkoj ravnoteži sa zidovima šupljine, pa koliko ga zidovi apsorbiraju, isto ga toliko vraćaju natrag u šupljinu emitirajući zračenje. Dakle, u termičkoj ravnoteži na temperaturi T, u šupljini se nalazi stalan iznos energije zračenja, koji po jedinici volumena označimo s U_T. Njemu doprinose svi modovi titranja elektromagnetskog polja, dakle zračenje svih frekvencija, pa pišemo

$$U_T = \int^{\infty}_{0} u_T(\nu) d \nu \,$$ (1.5)

gdje je $u_T(\nu) d\nu$ iznos energije zračenja frekvencije $\nu$ unutar infinitezimalnog intervala frekventnog intervala $d\nu$. Funkciju $u_T(\nu )$ nazivamo spektralnom gustoćom energije zračenja ili frekventnom distribucijom gustoće energije zračenja. Ta se spektralna gustoća može dati - što je naravno posve ekvivalentno - i kao funkcija valne duljine $\lambda = c/\nu$ (c je brzina svjetlosti u vakuumu). Vezu između te nove funkcije ${\widetilde u}_T(\lambda)$ i frekventne distribucije $u_T(\nu )$ nalazimo pomoću relacije $d\nu = - c \, d\lambda/\lambda^{2}$, te uvjeta da funkcija ${\widetilde u}_T(\lambda)$ mora u integralu po valnim duljinama $\lambda$ dati istu gustoću energije U_T kao što je daje integral po frekvencijama (1.5). Odmah slijedi veza (vidi zadatak 1.2.1)

$${\widetilde u}_T(\lambda) = u_T(\nu) \frac{c}{\lambda^{2}} = u_T(c/\lambda) \frac{c}{\lambda^{2}}.$$ (1.6)

Eksperimentalno, šupljinsku spektralnu gustoću $u_T(\nu )$(odnosno ${\widetilde u}_T(\lambda)$) možemo dobiti ako proučavamo zračenje iz otvora na zidu šupljine koja je u termodinamičkoj ravnoteži na temperaturi T. Naime, egzaktno geometrijsko razmatranje dokazuje da je izračena snaga, tj. energija izračena u jedinici vremena iz otvora jedinične površine, dana s P_T=(c/4)U_T, kao i da je spektralna gustoća izračene snage (tj. frekventna distribucija te snage) $p(\nu)$ na isti način proporcionalna šupljinskoj spektralnoj gustoći:

$$p_T(\nu) = \frac{c}{4} \, u_T(\nu) \, , \quad {\rm te \quad naravno \quad} P_T = \int^{\infty}_{0} p_T(\nu) d \nu \, .$$ (1.7)

Tako su Lummer i Pringsheim 1899 i 1900, a Rubens i Kurlbaum 1900 godine, izmjerili $u_T(\nu )$ s dovoljnom točnošću da klasičnu teoriju stave na odlučnu kušnju.

Za nekoliko vrijednosti parametra temperature T, rezultati eksperimenata takvog tipa prikazani su na Slici 1.1. Iz razloga datih gore, te krivulje možemo u izvrsnoj aproksimaciji smatrati spektralnom gustoćom energije zračenja crnog tijela. Pitanje je možemo li ih dobiti i teorijski.

  

Figure: Spektralne gustoće energije zračenja $u_T(\nu )$, u jedinicama 10^-15 $\rm Joule\cdot s/m^3$, za četiri temperature: T=4000 K, T=5000 K, T=6000 K i T=7000 K. Frekvencije $\nu$ su dane u jedinicama 10¹⁴ Hz. Kako temperature rastu, dobivamo sve više krivulje, a maksimumi im se pomiču na veće frekvencije.

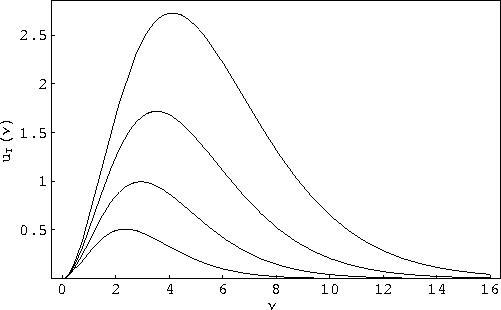Wien je 1893. iz termodinamičkih razmatranja izveo svoj ``zakon pomaka", prema kojemu se ona frekvencija, odnosno ona valna duljina $\lambda = c/\nu$ za koju je spektralna gustoća energije zračenja crnog tijela maksimalna, nalazi na vrijednosti $\lambda_{max}$ koja ovisi samo o temperaturi crnog tijela:

$$\lambda_{max} = \frac{{\rm konstanta}}{T} \, .$$ (1.8)

Općenito, iz Wienovih termodinamičkih razmatranja slijedilo je da spektralna gustoća energije mora imati oblik

$${\widetilde u}_T^{(W)} (\lambda) = \frac{W (\lambda T)}{\lambda^{5}}$$ (1.9)

gdje je $W (\lambda T)$ funkcija koja je tada ostala neodređena, jer se njen oblik nije mogao odrediti samo iz termodinamičkih razmatranja, već su bile potrebne neke pretpostavke o mehanizmu nastanka zračenja. Kasnije je Wien pomoću takvih pretpostavki - od kojih su neke bile više, a neke manje plauzibilne - predložio oblik $W (\lambda T)= K_1 \exp(-K_2/\lambda T)$, gdje su K₁ i K₂ konstante. Dakle, specifičniji oblik Wienovog zakona bi bio

$${\widetilde u}_T^{(W)}(\lambda) = K_1 \frac{\exp(-K_2/\lambda T)}{\lambda^{5}} \, ,$$ (1.10)

što se eksperimentalno pokazalo dobrim asimptotskim oblikom za kratke valne duljine (tj. visoke frekvencije), ali se nikako nije slagalo s eksperimentalnim u_T za duge valne duljine, odnosno niske frekvencije. Treba međutim primjetiti, da zbog specifičnih pretpostavki u izvodu izraza (1.10), on ima mnogo manju ``teorijsku težinu" od općenitog oblika Wienovog zakona (1.9).

Najvažniji pokušaj da se izvede $u_T(\nu )$na temelju pretpostavki klasične fizike doveo je do Rayleigh-Jeansovog zakona zračenja, naime

$$u_T^{(RJ)}(\nu) = \frac { 8 \pi \nu^{2}}{c^{3}} k_{B} T \, ,$$ (1.11)

gdje je $k_{B} = 1.381 \times 10^{-16}$ erg/K Boltzmannova konstanta.

Rayleigh-Jeansova formula (1.11) za gustoću zračenja u šupljini koja predstavlja crno tijelo, može se već u početnim kolegijima kao što je Opća Fizika izvesti iz pretpostavke da zračenje u toj šupljini potječe od oscilacija naboja vezanih harmoničkim silama^1.1 u materijalu zidova. Kome se ta pretpostavka čini previše specijalizirana, tako da ne može dovesti do iole općenite predikcije, ili čak previše nategnuta, tako da možda dovede do spurioznih rezultata, neka se prisjeti da se gibanja vrlo kompliciranih sustava mogu analizirati preko rastava u normalne modove (za male pomake, kada međučestične sile u dobroj aproksimaciji možemo smatrati linearnim funkcijama pomaka od ravnotežne točke), a ti su normalni modovi ekvivalentni harmoničkim oscilatorima. Nadalje, odmah možemo uočiti jednu indiciju da je rezultat (1.11) zapravo vrlo općenit, a to je da naboj oscilatora, njegova masa, sva druga specifična svojstva nekog oscilatora, u njemu nisu prisutna - pokratila su se. Osim toga, isti rezultat (1.11) se može izvesti i bez pretpostavke o harmoničkim oscilacijama naboja u materijalu zidova. Ekvivalentan, ali jasnije prihvatljiv - i zato najčešće korišten^1.2 - pristup je da s $\hat{\rm a}$mo polje elektromagnetskog zračenja prikažemo kao skup harmoničkih oscilatora. Naime, znamo da se svaki val Fourierovom analizom dade izraziti kao odgovarajuća superpozicija harmoničkih valova - normalnih modova, pa se nastanak tog valnog polja može pripisati odgovarajućem broju harmoničkih oscilatora. Uočimo da se elektromagnetsko zračenje u šupljini - ako je zaista u termodinamičkoj ravnoteži sa zidovima te šupljine savršeno reflektirajućih zidova - mora sastojati od stojnih valova. Rayleigh-Jeansov zakon (1.11) se dobije ako se točno izračuna koliki je broj tih stojnih valova po jedinici volumena za svaku frekvenciju, i ako svakoj takvoj nezavisnoj vibraciji pridjelimo prosječnu energiju k_B T u skladu s principom ekviparticije energije u klasičnoj statističkoj fizici. Naime, za harmonički oscilator s jednim stupnjem slobode, prosječna potencijalna energija je $\frac{1}{2} k_{B} T$, kao i prosječna kinetička. Dakle, u prosječnoj energiji jednog stupnja slobode harmoničkog oscilatora u klasičnoj statističkoj fizici leži porijeklo faktora k_B T u Rayleigh-Jeansovom zakonu (1.11).

Ovime želimo naglasiti da je proučavanje i izvođenje klasične gustoće zračenja na sve moguće načine pokazalo da je Rayleigh-Jeansov zakon (1.11) točan, općenit i neizbježan rezultat klasične fizike, a ne plod neke greške ili nekih posebnih pretpostavki koje bi ga ograničile na neku specijalnu situaciju. To je važno naglasiti, jer je on baš zato i katastrofalan za klasičnu fiziku, premda se slaže s eksperimentalnim podacima bar za niske frekvencije i premda je oblika (1.9) kakav traži općeniti Wienov zakon. Iako naravno važno, pritom nije najkatastrofalnije to što se formula (1.11) ne slaže s eksperimentalnim podacima za visoke frekvencije, nego je najvažnije kakvo je to neslaganje. Dakle, najvažnije je to što je očigledno apsurdno da na svakoj temperaturi T > 0, spektralna gustoća energije zračenja monotono raste s frekvencijom do u beskonačnost kao $\nu^2$. To znači da bi šupljina na konačnoj temperaturi T sadržavala po jedinici volumena energiju zračenja U_T beskonačnog iznosa. Kad bismo takvu šupljinu - recimo ugašenu pećnicu na sobnoj temperaturi - otvorili, iz nje bi prema Rayleigh-Jeansovu zakonu (1.11) trebalo da sine ne samo dugovalna i infracrvena, nego i vidljiva svjetlost, te još puno više ultraljubičastog (i još daleko više X- i $\gamma$-) zračenja. Ta besmislena predikcija naziva se ultraljubičasta katastrofa, a budući da je u klasičnoj fizici neizbježna, znači da je klasična fizika nesposobna opisati zračenje crnog tijela. Greška nije dakle u izvodu formule (1.11), već u pretpostavci da se na zračenje crnog tijela mogu primijeniti zakoni klasične fizike.

Gdje je rješenje? Interesantno je da je već James Jeans - inače znanstvenik koji je u kinetičkoj teoriji plinova dokazao zakon ekviparticije energije - bio na pravom tragu, ali naravno ne kod zračenja crnog tijela, već u jednom drugom, samo naizgled potpuno drugačijem problemu. Taj problem je onaj spomenut na samom početku ovog poglavlja, naime toplinski kapaciteti plinova koje su uznemiravale Maxwella: zaista, problem je da one nikako ne mogu biti konzistentne s kinetičkom teorijom plinova ako vijedi zakon ekviparticije energije, da na temperaturi T svaki nezavisni vibracioni stupanj slobode sistema ima prosječnu energiju $\langle E \rangle = k_{B} T$ (jer harmonički oscilator ima prosječnu kinetičku energiju $\frac{1}{2} k_{B} T$ i prosječnu potencijalnu energiju $\frac{1}{2} k_{B} T$). Jeans je uočio da bi problem bio riješen kad bi se visokofreventne vibracije molekula plina s padom temperature ``zamrzavale", tj. otpadale kao relevantni stupnjevi slobode jer ih se na preniskoj temperaturi ne bi moglo pobuditi.

Kod ``ultraljubičaste katastrofe", zbog same prirode tog problema, očito je još plauzibilnije nego kod toplinskih kapaciteta plinova, da problem nastaje zbog precjenjivanja doprinosa visokofrekventnih oscilacija, koje vjerojatno zapravo uopće ne mogu biti pobuđene ako je temperatura preniska, i zato nemaju energiju k_B T. Ali gdje pronaći, kako dobiti nekakav mehanizam za gušenje doprinosa visokih frekvencija? U klasičnoj fizici ga nije bilo - u stvari, na temelju njenih zakona pojavljivalo se baš suprotno: ekviparticija energije $\langle E \rangle = k_{B} T$.

Doduše, u Wienovom specijalnijem zakonu (1.10) takvo gušenje je prisutno. Međutim, Wien je pri izvodu te spektralne gustoće (1.10) takvo gušenje implicite sam unio (``rukom", u fizičarskom žargonu) pomoću svojih pretpostavki^1.3 o mehanizmu zračenja. Naime, on je pretpostavio da to zračenje potječe od molekula za čije brzine vrijedi Maxwellova raspodjela,

$$P(v) = 4\pi \left(\frac{m}{2\pi k_B T}\right)^{\frac{3}{2}} v^2 {\Large {\rm e}}^{-\frac{m v^2}{2 k_B T}} \, ,$$ (1.12)

ali i da te molekule u interval frekvencija $[\nu,\nu+d\nu]$ mogu zračiti samo ako su im brzine u intervalu [v,v+dv], te da je intenzitet zračenja proporcionalan broju molekula koje zrače. Time se očito u spektralnu raspodjelu po frekvencijama ili valnim duljinama mora prenijeti eksponencijalno prigušenje koje je u Maxwellovoj raspodjeli prisutno za brzine. Međutim, iako na pravom tragu jer je pokušavao dobiti potrebno gušenje visokih frekvencija, Wien tim svojim pretpostavkama očito nije uspio ``napipati" neki fizikalni zakon od fundamentalnog značaja, jer spektralna raspodjela (1.10) koja iz njih slijedi nije dobra na nižim (a ni na srednjim) frekvencijama.

Potpuno drugačijeg karaktera je ono što je pretpostavio Planck. On je uspio dobiti pravu prosječnu vrijednost energije harmoničkog oscilatora, koja će zamijeniti $\langle E \rangle = k_{B} T$ u Rayleigh-Jeansovoj formuli, tako što je pretpostavio nešto što se pokazalo u najdubljem smislu riječi fundamentalnim zakonom prirode, iako u suprotnosti s klasičnom fizikom. Tako je počelo otkrivanje kvantne fizike.

Planck je uvidio da eksperimentalne gustoće energije zračenja može teorijski reproducirati samo ako pretpostavi nešto, sa stanovišta dotad poznate fizike vrlo neobično - naime, da harmonički oscilator prirodne frekvencije $\nu$ može emitirati i apsorbirati energiju samo u diskretnim porcijama, u kvantima energije $E_\nu = h\nu$, gdje je h nova fundamentalna konstanta, kasnije prozvana Planckova konstanta. Dakle, energija zračenja frekvencije $\nu$ može postojati samo u cjelobrojnim multiplima od $E_\nu = h\nu$. Isto tako, to znači da harmonički oscilator frekvencije $\nu$ ne može imati bilo kakvu energiju, već samo energije na diskretnim nivoima razmaknutim za taj elementarni inkrement energije $h \nu$. To međutim znači negiranje dotad poznatih, ``klasičnih" zakona fizike, jer je u oštroj suprotnosti s onim što vrijedi za klasični harmonički oscilator mase m i prirodne frekvencije $\nu$, čija energija

$$E_{{\rm klas}} = \frac{1}{2} m \left(\frac{dx}{dt}\right)^2 +... ...{4\pi^2 \nu^2}{2} x^2 = \frac{4\pi^2 \nu^2}{2} {x_{\rm max}}^2$$ (1.13)

može biti bilo kakva, izražena kontinuiranim veličinama kakva je maksimalna elongacija $x_{\rm max}$. Prema Planckovoj hipotezi to nije točno, odnosno može biti točno samo u ograničenom smislu, u limesu $h\to 0$, tj. u situacijama kada je veličina Planckove konstante zanemariva relativno prema drugim relevantnim veličinama. Tada bi i diskretne dozvoljene energije Planckovog ``kvantnog" harmoničkog oscilatora, razmaknute za kvant energije $E_\nu = h\nu$, ponovo prešle u kontinuum. Međutim, problem zračenja crnog tijela očito ne spada u takve situacije (osim za razmjerno niske frekvencije), i upravo je Planckova kvantna hipoteza donijela njegovo rješenje koje ćemo sad izložiti.

Pretpostavimo da su moguće energije harmoničkog oscilatora razmaknute ekvidistantno. Osnovno stanje ima najnižu energiju E₀, a beskonačno visoka ljestvica pobuđenih stanja neka ima energije $E_1=E_0+h\nu$, $E_2=E_1+h\nu=E_0+2h\nu$, $E_3=E_2+h\nu=E_0+3h\nu$, $E_4=E_3+h\nu=E_0+4h\nu$, ..., itd. Iako ćemo u toku ovog kursa vidjeti da zapravo $E_0\neq 0$, te da to za neka fizikalna pitanja ima značaja, ovdje možemo mirno preuzeti Planckovu pretpostavku E₀=0, jer u ovom su slučaju važne samo razlike energija između mogućih nivoa. (Svaka konkretna vrijednost E₀ ima samo značenje izbora referentnog ishodišta od kojeg računamo energiju, a za $E_0\neq 0$ se lako vidi da bi u donjem izvodu prosječne energije oscilatora pridonijela samo temperaturno neovisan član koji je isti za svaku točku svemira i ima značenje energije vakuuma, pa je irelevantan za gustoću zračenja crnog tijela.) Planck je nadalje pretpostavio da je vjerojatnost zauzeća pojedinog nivoa data Boltzmannovom raspodjelom. Prema tome, ako s P₀ označimo vjerojatnost da je neki oscilator u osnovnom stanju, vjerojatnost da je u n-tom višem dozvoljenom stanju iznosi

$$P_n = P_0 \, {\Large {\rm e}}^{-(E_n - E_0)/k_B T} = P_0 \, {\Large {\rm e}}^{-nh\nu/k_B T} \, .$$ (1.14)

Ako je N₀ broj oscilatora (po jedinici volumena) u osnovnom stanju, onda ih u prvom pobuđenom stanju, dakle s energijom E₁, ima $N_1 = N_0 \exp(-h\nu/k_B T)$, u drugom $N_2 = N_0 \exp(-2h\nu/k_B T)$, itd. Općenito, u n-tom stanju, na energiji E_n, ima ih $N_n = N_0 \exp(-nh\nu/k_B T)$. Uvedimo pokratu $x\equiv \exp(-h\nu/k_B T)$. Ukupni broj kvantnih oscilatora prirodne frekvencije $\nu$ tad možemo pisati $N_{ukupni} = N_0 \, (1 + x + x^2 + x^3 + ...) = N_0 / (1 - x)$. Ukupna njihova energija je $E_{ukupna} = N_0 \, h \nu \, (0 + x + 2x^2 + 3x^3 + ...) = N_0 \, h \nu \, x/(1 - x)^2$, gdje smo konačno upotrijebili i E₀=0. Prosječna energija je po definiciji

$$\langle E \rangle \equiv \frac{E_{ukupna}}{N_{ukupni}} = h \nu \frac{x}{1-x} .$$ (1.15)

Slijedi da je za harmonički oscilator prirodne frekvencije $\nu$, kvantna predikcija za prosječnu energiju

$$\langle E \rangle = \frac{h \nu}{{\Large {\rm e}}^{h \nu/k_{B} T} - 1 }$$ (1.16)

To je ono što zamjenjuje klasičnu predikciju k_B T u općenitom slučaju, a na nju se reducira za $h \nu << k_{B} T$, dakle kada je elementarni kvant energije mnogo manji od tipične energije termalnog gibanja. Inače, (1.16) je prva poznata formula kvantne fizike. Kada dakle u Rayleigh-Jeansovom zakonu (1.11) umjesto k_B T upotrijebimo (1.16), dobivamo Planckov zakon zračenja

$$u_T(\nu) = \frac{8 \pi h \nu^{3}}{c^{3}} \frac{1}{{\Large {\rm e}}^{h \nu/k_{B} T} - 1 } \, .$$ (1.17)

Ovaj zakon se slaže s eksperimentalnim gustoćama zračenja crnog tijela za sve frekvencije i temperature za Planckovu konstantu iznosa

$$h = 6.626 \times 10^{-27} {\rm erg \cdot s} \, .$$ (1.18)

Tako je - prilagođujući Planckovu teorijsku krivulju eksperimentalnim spektralnim gustoćama energije zračenja crnog tijela - po prvi put izmjerena ova fundamentalna konstanta prirode.

Zadaci

1.) Spektralne gustoće zračenja koje su dane kao funkcije valne duljine izrazi kao funkcije frekvencije, i obratno. Time ćeš dokazati formulu (1.6).

2.) Koje spektralne gustoće zračenja zadovoljavaju oblik (1.9) koji zahtjeva Wienov zakon iz 1893?

3.) Provjeri da Planckov zakon zračenja u odgovarajućim graničnim slučajevima daje Rayleigh-Jeansov zakon, odnosno Wienov zakon iz 1896.

4.) Pokaži da Planckov zakon zračenja (1.17) preko formula (1.7) daje Stefanov zakon $P_T = \sigma T^4$, te da predviđa da je Stefan-Boltzmannova konstanta $\sigma = 2\pi^5 k_B^4/15 h^3 c^2$. Izračunaj njenu (empirički provjerenu) vrijednost $\sigma = 5,67 \cdot 10^{-8}$ W/m² K⁴.