5.2. Elektrodinamika

Zadatak E-1

Potencijal \(\phi(\vec{r})\), u točki \(\vec{r}=(x, y, z)\) koji je posljedica statičke raspodjele N nabijenih čestica s nabojima \(q_1, q_2, \ldots, q_N\) i položajima \(\vec{r}_1 = (x_1, y_1, z_1)\), \(\vec{r}_2 = (x_2, y_2, z_2)\),..., \(\vec{r}_N = (x_N, y_N, z_N)\) je dan formulom:

\[\phi(x, y, z) = \sum_{k=1}^{N} \frac{q_k}{|\vec{r} - \vec{r}_k|} \,.\]

Definirajte funkciju plotpot(naboji, xgranice, ygranice) koja crta ekvipotencijalne konture u ravnini \(z=0\), gdje su naboji i njihovi položaji zadani kao lista oblika \([(q_1, x_1, y_1, z_1), (q_2, x_2, y_2, z_2), \ldots ]\). Upotrijebite tu funkciju da nacrtate ekvipotencijalne konture za naboje [(-1, 1, 1, 1), (+1, -1, -1, 0.3), (+1, -1, 1, 0.5)].

Naputak: Koristite funkciju contour_plot() da nacrtate \(\phi(x, y, 0)\)

5.2.1. Zračenje ubrzavanog naboja

(Donji kod je napravljen za Sage sustav. Možete ga izvršiti ako instalirate Sage ili online na sagemathcloud-u. Dobra je vježba konvertirati to u Jupyter/Python.)

Snaga zračenja po prostornom kutu za točkasti naboj \(q\) brzine \(\vec{\beta}\) (u jedinicama brzine svjetlosti \(c\)) i ubrzanja \(\vec{a}\) dana je Poyntingovim vektorom:

\[\frac{dP}{d\Omega} = \frac{q^2 a^2}{16 \pi^2 \epsilon_0 c^3}\frac{|\hat{n}\times ((\hat{n}-\vec{\beta})\times\hat{a})|^2}{(1-\hat{n}\cdot\vec{\beta})^5} \;.\]

gdje je \(\hat{n}\) jedinični vektor u smjeru promatrača, a \(\hat{a}\) jedinični bezdimenzionalni vektor ubrzanja. Cf. npr. Griffits, Eq. (11.72)

sage: var('theta phi')
(theta, phi)

sage: def unitn(theta, phi):
....:     """Unit vector \hat{n} in Cartesian coordinate system."""
....:
....:     return vector((sin(theta)*cos(phi), sin(theta)*sin(phi),
....:                                                     cos(theta)))

Funkcija poynting() definira samo drugi bezdimenzionalni faktor u gornjem izrazu koji opisuje kutnu ovisnost

sage: def poynting(theta, phi, beta, ahat):
....:     """Angular part of Poynting vector."""
....:
....:     nk = unitn(theta, phi)
....:     num = (nk.cross_product((nk-beta).cross_product(ahat))).norm()^2
....:     denom = (1-nk.dot_product(beta))^5
....:     return (num/denom) * nk

sage: def poynting2d(theta, v, a):
....:     """Projection of Poynting vector on phi=0, i.e x-z plane."""
....:
....:     p = poynting(theta, 0, v, a)
....:     return (p[0], p[2])

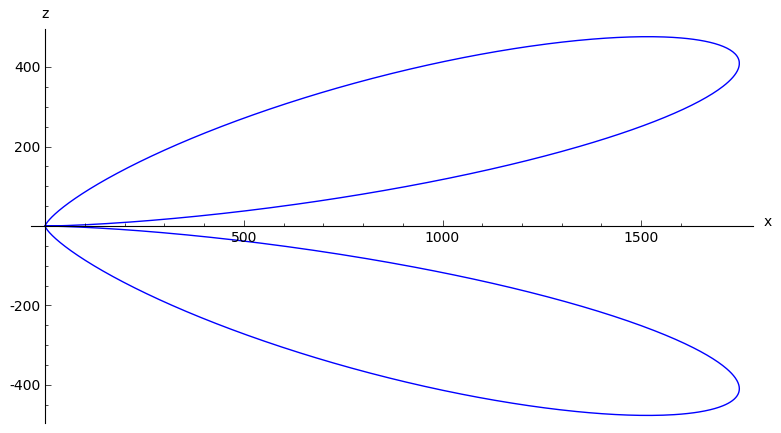
Zračenje kad je akceleracija u smjeru brzine. Cf. Griffits, slika 11.14.

sage: parametric_plot(poynting2d(theta, vector((0.9, 0, 0)),
....:     vector((1, 0, 0))), (theta, 0, 2*pi), axes_labels=['x', 'z'])

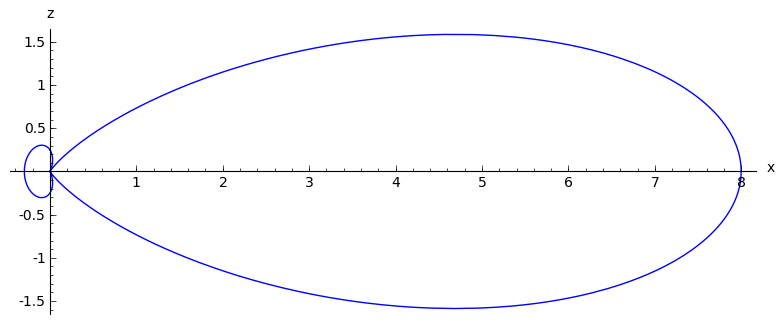
Sinhrotronsko zračenje, kad je akceleracija okomita na brzinu. Cf. Griffits, slika 11.16.

sage: parametric_plot(poynting2d(theta, vector((0.5, 0, 0)),
....:    vector((0, 0, 1))), (theta, 0, 2*pi), axes_labels=['x', 'z'])

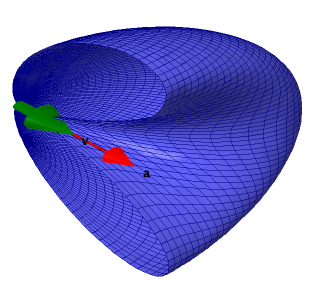
sage: def plotField(v=vector((0.5, 0, 0)), a=vector((1, 0, 0))):
....:     """Plot the 3D shape of radiation field (cut along x-z plane)."""
....:
....:     R = parametric_plot3d(poynting(theta, phi, v, a), (theta, 0, pi),
....:          (phi, 0, pi), plot_points=[100,100], frame=False, opacity=0.7)
....:     Av = arrow3d((0,0,0), 3*v, color='green', width=5)
....:     Aa = arrow3d((0,0,0), 3*a, color='red', width=3)
....:     Tv = text3d("v", 3.6*v, size=15)
....:     Ta = text3d("a", 3.3*a, size=50)
....:     return R + Av + Aa +Tv + Ta

sage: plotField().show(mesh=True)

5.2.2. Ukupna snaga zračenja za sinhrotronsko zračenje:

Za elektron u magnetskom polju \(B\), okomitom na njegovu trenutnu brzinu, ubrzanje usljed Lorentzove sile je

\[a = \frac{qc\beta B}{m_e} \;.\]

Nakon uvrštavanja, rezultat je zgodno izraziti preko Thomsonovog udarnog presjeka

\[\sigma_{T} = \frac{2 \mu_0 e^4}{12 \pi m_{e}^2 \epsilon_0 c^2} = 6.652 \, {\rm m}^2 \;,\]

i gustoće energije magnetskog polja

\[U_{B} = \frac{B^2}{2 \mu_0} \;,\]

pa se konačno dobije za ukupnu snagu zračenja:

\[P = \frac{3}{4 \pi} \sigma_T c \beta^2 U_B \int d\Omega \frac{|\hat{n}\times ((\vec{n}-\vec{\beta})\times\hat{a}|^2}{(1-\hat{n}\cdot\vec{\beta})^5} \;.\]

Iskoristiti ćemo ovaj primjer za demonstraciju računanja s mjernim jedinicama upotrebom SciPy modula constants i Pythonovog modula units.

sage: from scipy import constants
sage: c = constants.c * (units.length.meter / units.time.second)
sage: q = units.charge.elementary_charge
sage: sigmaT = constants.physical_constants['Thomson cross section'
....:                                         ][0] * units.length.meter^2
sage: mu0 = constants.mu_0
sage: print "Thomsonov udarni presjek = " + str(sigmaT)
Thomsonov udarni presjek = (6.652458734e-29)*meter^2

sage: UB(B) = B^2/2/constants.mu_0 * (units.energy.joule/units.length.meter^3)

Relevantni integral po prostornom kutu:

sage: def Kint(v=vector((0.5, 0, 0)), a=vector((0, 0, 1))):
....:     return integral_numerical(lambda theta: sin(theta) *
....:       integral_numerical(lambda phi: poynting(theta, phi, v,
....:          a).dot_product(unitn(theta, phi)), 0, 2*pi)[0], 0, pi)[0]

sage: def pwr(beta, B):
....:     return (3/4/pi.n()) * sigmaT * c * beta^2 * UB(B) * Kint(
....:                                              v=vector((beta,0,0)))

sage: print "Ukupna snaga zracenja = " + str(pwr(0.5, 1))
Ukupna snaga zracenja = (7.05359483944320e-15)*joule/second

Za kontrolu uspoređujemo s formulom

\[P = 2 \sigma_T \beta^2 \gamma^2 c U_B\]

sage: gamma(beta) = 1/(1-beta^2)
sage: pwr2(beta, B) = 2 * sigmaT * beta^2 * gamma(beta)^2 * c * UB(B)

sage: pwr2(0.5, 1.)
(7.05359483944320e-15)*joule/second