5.1. Mehanika

Zadatak M-1

Neka na česticu u ravnini djeluje potencijal \(U(x,y)= -4 x^2 y^3\). Nacrtajte ekvipotencijalne konture ovog potencijala. Nadalje, rješavajući numerički Newtonovu diferencijalnu jednadžbu gibanja, pronađite putanju čestice, uz početne uvjete \(x(0)=y(0)=-1, v_x(0)=2, v_y(0)=-3\), od trenutka \(t=0\) do trenutka \(t=1.43\). Nacrtajte tu putanju, a onda je pokušajte superponirati na gore dobivene konture potencijala. Igrajte se malo s početnim uvjetima i uvjerite se da je sve OK. Grafički usporedite kinetičku, potencijalnu i ukupnu energiju u ovisnosti o vremenu.

Zadatak M-2

Formule za nerelativističku i relativističku kinetičku energiju tijela mase m koje se giba brzinom v su

\[K_{\rm nr} = \frac{1}{2} m v^2 \;, \qquad K_{\rm rel} = m c^2 \left( \frac{1}{\sqrt{1-v^2/c^2}}-1\right) \;.\]

1. Definirajte odgovarajuće funkcije knr(v) i krel(v) te usporedite na istom dijagramu ponašanje tih funkcija za brzine od 0 do \(3\cdot 10^8\) m/s za jediničnu vrijednost mase. Označite veličine i njihove jedinice na koordinatnim osima!
2. Odredite brzinu pri kojoj je greška nerelativističke formule tisućinku promila.
3. Da li se knr(v) i krel(v) slažu za male vrijednosti brzine? Ako ne, korigirajte krel() da postignete slaganje.

5.1.1. Problem tri tijela

Numeričkim rješavanjem Newtonovih jednadžbi simuliramo gibanje tri tijela koja gravitiraju, a čije je gibanje ograničeno na x-y ravninu. Radimo s jediničnim masama i G=1 vrijednošču Newtonove gravitacijske konstante. Za tri tijela u dvodimenzionalnoj ravnini imamo 6 diferencijalnih jednadžbi drugog reda koje pretvaramo u 12 diferencijalnih jednadžbi prvog reda. Donji kod je napravljen za Sage sustav. Možete ga izvršiti ako instalirate Sage ili online na sagemathcloud-u. Dobra je vježba konvertirati to u Jupyter/Python.

sage: def system(t, y):
....:     # y_i = (x1, y1, x2, y2, x3, y3
....:     #  i=     0   1   2   3   4   5
....:     #        vx1, vy1, vx2, vy2, vx3, vy3)
....:     #         6    7    8    9   10   11
....:     return [y[6], y[7], y[8], y[9], y[10], y[11],
....:     -((y[0] - y[2])/((y[0] - y[2])**2 + (y[1] - y[3])**2)**1.5) -
....:     (y[0] - y[4])/((y[0] - y[4])**2 + (y[1] - y[5])**2)**1.5,
....:     -((y[1] - y[3])/((y[0] - y[2])**2 + (y[1] - y[3])**2)**1.5) -
....:     (y[1] - y[5])/((y[0] - y[4])**2 + (y[1] - y[5])**2)**1.5,
....:     (y[0] - y[2])/((y[0] - y[2])**2 + (y[1] - y[3])**2)**1.5 -
....:     (y[2] - y[4])/((y[2] - y[4])**2 + (y[3] - y[5])**2)**1.5,
....:     (y[1] - y[3])/((y[0] - y[2])**2 + (y[1] - y[3])**2)**1.5 -
....:     (y[3] - y[5])/((y[2] - y[4])**2 + (y[3] - y[5])**2)**1.5,
....:     (y[0] - y[4])/((y[0] - y[4])**2 + (y[1] - y[5])**2)**1.5 +
....:     (y[2] - y[4])/((y[2] - y[4])**2 + (y[3] - y[5])**2)**1.5,
....:     (y[1] - y[5])/((y[0] - y[4])**2 + (y[1] - y[5])**2)**1.5 +
....:     (y[3] - y[5])/((y[2] - y[4])**2 + (y[3] - y[5])**2)**1.5,
....:     ]

Za početne uvjete uzimamo neke od 15 periodičkih orbita navedenih u Tablici 1 članka Šuvakov i Dmitrašinović, Phys. Rev. Lett. 110, 114301 (2013), dostupno online: arXiv:1303.0181.

sage: figure8=[[-1,0,1,0,0,0,0.347111,0.532728,0.347111,0.532728,-0.694222,
....:            -1.06546],[-1.05783,1.05784,-0.522919,0.522917],6.32445]
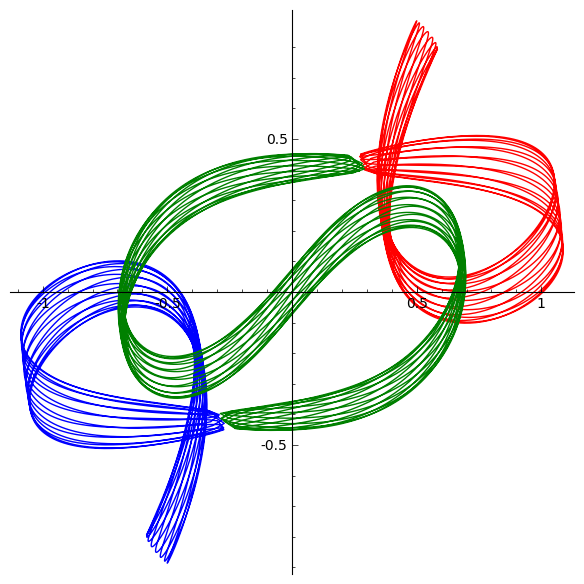
sage: goggles=[[-1,0,1,0,0,0,0.0833,0.127889,0.0833,0.127889,-0.1666,
....:            -0.255778], [-1.04973,1.04972,-0.738248,0.738249],10.4668]
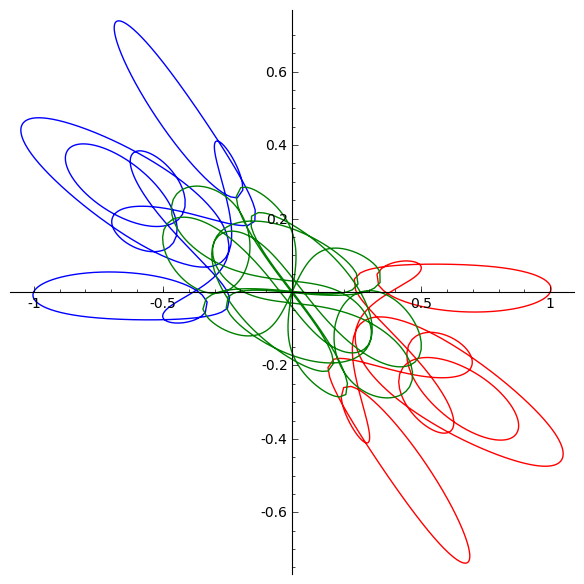
sage: butterfly2=[[-1,0,1,0,0,0,0.392955,0.097579,0.392955,0.097579,-0.78591,
....:               -0.195158],[-1.07444,1.07449,-0.174197,0.17414],7.00391]
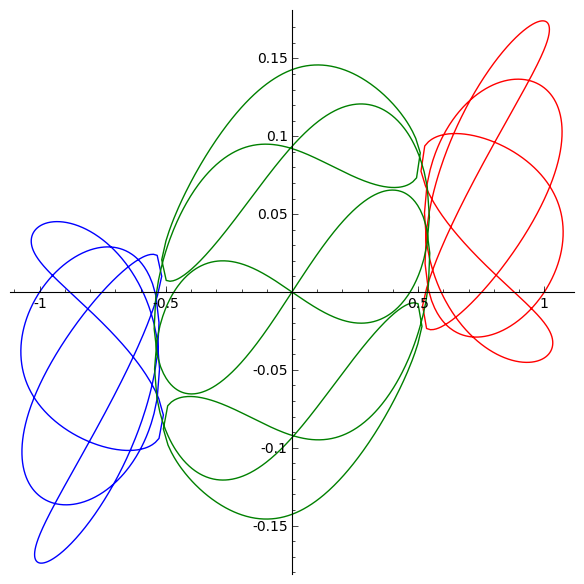
sage: yinyang2a=[[-1,0,1,0,0,0,0.416822,0.330333,0.416822,0.330333,
....:      -0.833644,-0.660666],[-1.0874,1.08734,-0.88595,0.885999],55.7898]

Umjesto odeint, koristit čemo ode_solver.

sage: S = ode_solver()
sage: S.function = system
sage: S.ode_solve(y_0=figure8[0], t_span=[0, figure8[2]], num_points=1000)
sage: sol_figure8 = S.solution
sage: S.ode_solve(y_0=goggles[0], t_span=[0, goggles[2]], num_points=2000)
sage: sol_goggles = S.solution
sage: S.ode_solve(y_0=butterfly2[0], t_span=[0, butterfly2[2]],
....:                                                     num_points=2000)
sage: sol_butterfly2 = S.solution
sage: S.ode_solve(y_0=yinyang2a[0], t_span=[0, yinyang2a[2]],
....:                                                     num_points=6000)
sage: sol_yinyang2a = S.solution

Također, umjesto crtanja Matplotlibom koristit ćemo Sageove grafičke elemente, konkretno primitivni grafički objekt line.

sage: G = Graphics()
sage: xshift = 0.005 # for visibility
sage: yshift = 0.01 # for visibility
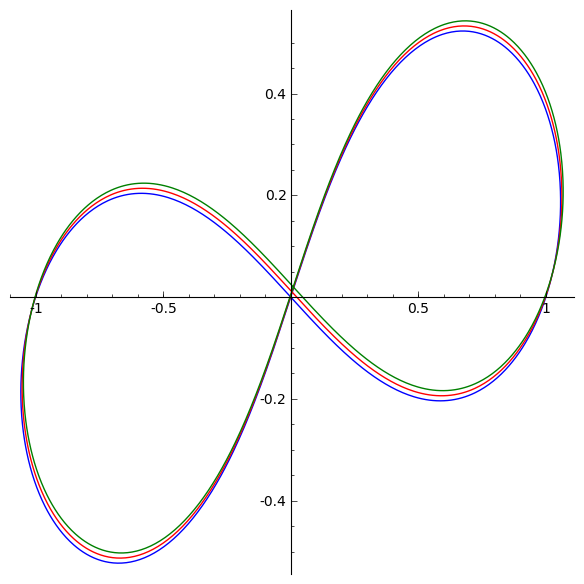
sage: G += line([(x[0],x[1]) for t,x in sol_figure8])
sage: G += line([(x[2]+xshift,x[3]+yshift) for t,x in sol_figure8],
....:                                                        color='red')
sage: G += line([(x[4]+2*xshift,x[5]+2*yshift) for t,x in sol_figure8],
....:                                                       color='green')
sage: show(G, figsize = [6,6])

sage: G = Graphics()
sage: G += line([(x[0],x[1]) for t,x in sol_goggles])
sage: G += line([(x[2],x[3]) for t,x in sol_goggles], color='red')
sage: G += line([(x[4],x[5]) for t,x in sol_goggles], color='green')
sage: show(G, figsize = [6,6])

sage: G = Graphics()
sage: G += line([(x[0],x[1]) for t,x in sol_butterfly2])
sage: G += line([(x[2],x[3]) for t,x in sol_butterfly2], color='red')
sage: G += line([(x[4],x[5]) for t,x in sol_butterfly2], color='green')
sage: show(G, figsize = [6,6])

sage: G = Graphics()
sage: G += line([(x[0],x[1]) for t,x in sol_yinyang2a])
sage: G += line([(x[2],x[3]) for t,x in sol_yinyang2a], color='red')
sage: G += line([(x[4],x[5]) for t,x in sol_yinyang2a], color='green')
sage: show(G, figsize = [6,6])