6. Dodaci

Donji kod je napravljen za Sage sustav. Možete ga izvršiti ako instalirate Sage ili online na sagemathcloud-u. Dobra je vježba konvertirati to u Jupyter/Python.

6.1. Testiranje hipoteze

Često je potrebno kvantificirati dobrotu neke prilagodbe te odrediti da li predloženi teorijski model dobro opisuje mjerenja. Uzmimo slijedeći niz mjerenja s greškama \((x_i, y_i, \sigma_i\equiv\Delta y_i\)):

sage: errdata = [[0.55, 0.74, 0.20], [0.9, 1.07, 0.12],
....:      [1.2, 1.28, 0.12], [1.5, 1.02, 0.12], [1.9, 1.63, 0.20]]
sage: xs = [x for x,y,err in errdata]
sage: ys = [y for x,y,err in errdata]
sage: errs = [err for x,y,err in errdata]

Za crtanje točaka s greškama (errorbars), koristimo Matplotlib funkciju errorbar() gdje greške idu u opcionalni argument yerr:

sage: import matplotlib.pyplot as plt
sage: import numpy as np
sage: fig, ax = plt.subplots(figsize=[5,3])

sage: ax.errorbar(xs, ys, yerr=errs, linestyle='None')
sage: fig.savefig('fig')

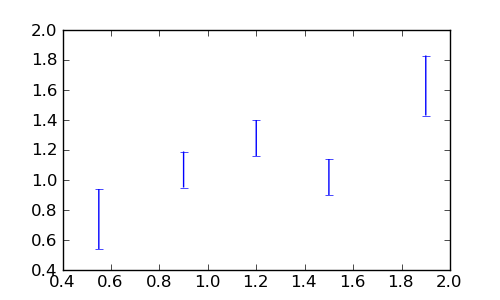
Promotrimo tri moguća teorijska opisa ovih mjerenja: potenciju \(x^a\), logaritam \(\log(a x)\) i obični pravac \(a + b x\) i odredimo parametre prilagodbom pomoću funkcije find_fit(). (Zasad zanemarimo različite greške pojedinih mjerenja.)

sage: var('a, b')
(a, b)
sage: powmodel(x) = x^a
sage: logmodel(x) = log(a*x)
sage: linmodel(x) = a*x+b

sage: powfit=find_fit([[x, y] for x,y,err in errdata], powmodel,
....:                             solution_dict=True); print powfit
{a: 0.6166290268412898}
sage: logfit=find_fit([[x, y] for x,y,err in errdata], logmodel,
....:                             solution_dict=True); print logfit
{a: 2.836898540272243}
sage: linfit=find_fit([[x, y] for x,y,err in errdata], linmodel,
....:                                   solution_dict=True); linfit
{b: 0.49690475972372317, a: 0.5380952396683008}

sage: xvals = np.linspace(0.4, 2)
sage: ax.plot(xvals, [powmodel(x).subs(powfit).n() for x in xvals],'r')
sage: ax.plot(xvals, [logmodel(x).subs(logfit).n() for x in xvals],'b-.')
sage: ax.plot(xvals, [linmodel(x).subs(linfit).n() for x in xvals],
....:                                   color='black', linestyle=':')
sage: fig.savefig('fig')

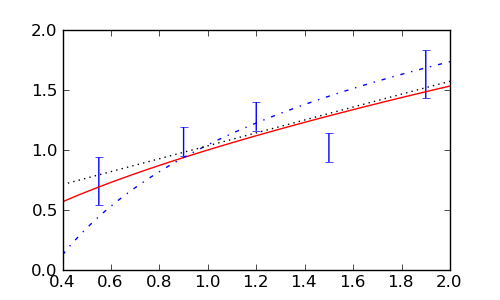
Teško je “od oka” procijeniti koji je opis najbolji, a još teže koji opisi su prihvatljivi a koji nisu. Standardna mjera dobrote fita je

\[\chi^2 = \sum_i \frac{(y_i - f(x_i))^2}{\sigma_{i}^2}\]

gdje su \(\sigma_i\) greške mjerenja. (Usput, kad je riječ o mjerenju frekvencija onda je greška dana kao \(\sigma_i=\sqrt{y_i}\).). Dobre su prilagodbe s \(\chi^2 \approx df\), gdje je \(df\) broj stupnjeva slobode (broj mjerenja minus broj slobodnih parametara funkcije koju prilagođavamo). Za točnije kvantificiranje dobrote prilagodbe gleda se integral statističke \(\chi^2\) raspodjele s \(df\) stupnjeva slobode od izračunatog \(\chi^2\) do beskonačnosti koji se često zove \(p\)-vrijednost i koji ne bi trebao biti manji od 0.1 ili barem 0.01 ili hipotezu treba odbaciti. Taj integral je implementiran kao funkcija scipy.stats.chisqprob(chisq, df). (Inače, za razliku od ovog primjera gdje tražimo statističku podršku hipotezi da funkcije opisuju mjerenja, često smo u obrnutoj situaciji gdje testiramo tzv. nul-hipotezu. Tu se npr. pitamo koja je vjerojatnost nekih mjerenja ukoliko neka čestica ne postoji ili ukoliko neki neki lijek ne djeljuje. Tada je mala p-vrijednost “poželjna” jer predstavlja statističku podršku postojanju te čestice ili dobrom djelovanju lijeka.)

Definirajmo tri funkcije koje prilagođavamo ...

sage: def powfun(p, x):
....:     return x^p[0]
....:
sage: def logfun(p, x):
....:     return log(p[0]*x)
....:
sage: def linfun(p, x):
....:     return p[1]*x+p[0]

... i odgovarajuću funkciju udaljenosti tj. odstupanja (čije kvadrate će minimizirati leastsq()). Tu trebamo staviti i težinski faktor \(1/\sigma_i\) za svaku točku kako bi točke s manjom greškom više utjecale na prilagodbu. Ovdje ćemo dodati još jedan argument putem kojeg ćemo prosljeđivati jednu od gornje tri funkcije:

sage: def dist(p, fun, data):
....:     return np.array([(y - fun(p, x))/err for (x,y,err) in data])

Definirajmo i odgovarajući \(\chi^2\):

sage: def chisq(p, fun, data):
....:     return sum( dist(p, fun, data)^2 )

Nakon minimizacije ćemo testirati i zastavicu ier tako da ukoliko leastsq() nije uspješna dobijemo odgovarajuću poruku o grešci:

sage: import scipy
sage: import scipy.stats
sage: fitfun = powfun
sage: ppow_final, cov_x, infodict, msg, ier = scipy.optimize.minpack.leastsq(
....:                dist, [1.],  (fitfun, errdata), full_output=True)
sage: if ier not in (1,2,3,4):
....:     print " -----> No fit! <--------"
....:     print msg
....: else:
....:     print "a =%8.4f +- %.4f" % (ppow_final, sqrt(cov_x[0,0]))
....:     chi2 = chisq([ppow_final], fitfun, errdata)
....:     df = len(errdata)-1
....:     print "chi^2 = %.3f" % chi2
....:     print "df = %i" % df
....:     print "p-vrijednost =  %.4f" % scipy.stats.chisqprob(chi2, df)
a =  0.5055 +- 0.1486
chi^2 = 7.880
df = 4
p-vrijednost =  0.0961

sage: fitfun = logfun
sage: plog_final, cov_x, infodict, msg, ier = scipy.optimize.minpack.leastsq(
....:               dist, [1.],  (fitfun, errdata), full_output=True)
sage: if ier not in (1,2,3,4):
....:     print " -----> No fit! <--------"
....:     print msg
....: else:
....:     print "a =%8.4f +- %.4f" % (plog_final, sqrt(cov_x[0,0]))
....:     chi2 = chisq([plog_final], fitfun, errdata)
....:     df = len(errdata)-1
....:     print "chi^2 = %.3f" % chi2
....:     print "df = %i" % df
....:     print "p-vrijednost =  %.4f" % scipy.stats.chisqprob(chi2, df)
a =  2.7219 +- 0.1693
chi^2 = 15.973
df = 4
p-vrijednost =  0.0031

sage: fitfun = linfun
sage: plin_final, cov_x, infodict, msg, ier = scipy.optimize.minpack.leastsq(
....:          dist, [1., 1.],  (fitfun, errdata), full_output=True)
sage: if ier not in (1,2,3,4):
....:     print " -----> No fit! <--------"
....:     print msg
....: else:
....:     parerrs = sqrt(scipy.diagonal(cov_x))
....:     print "p[0] =%8.3f +- %.4f" % (plin_final[0], parerrs[0])
....:     print "p[1] =%8.3f +- %.4f" % (plin_final[1], parerrs[1])
....:     chi2 = chisq(plin_final, fitfun, errdata)
....:     df = len(errdata)-2    # dva parametra
....:     print "chi^2 = %.3f" % chi2
....:     print "df = %i" % df
....:     print "p-vrijednost =  %.4f" % scipy.stats.chisqprob(chi2, df)
p[0] =   0.656 +- 0.2121
p[1] =   0.398 +- 0.1683
chi^2 = 7.116
df = 3
p-vrijednost =  0.0683

sage: fig, ax = plt.subplots(figsize=[5,3])
sage: ax.errorbar(xs, ys, yerr=errs, linestyle='None')
sage: xvals = np.linspace(0.4, 2)
sage: ax.plot(xvals, [powfun([ppow_final], x) for x in xvals],'r')
sage: ax.plot(xvals, [logfun([plog_final], x) for x in xvals],'b-.')
sage: ax.plot(xvals, [linfun(plin_final, x) for x in xvals], color='black',
....:             linestyle=':')
sage: fig.savefig('fig')

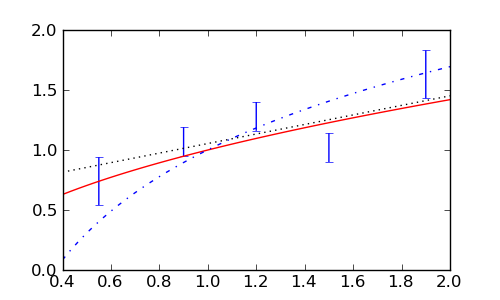
Ova analiza sugerira da možemo odbaciti logaritamski model, dok su druga dva modela, u nedostaku boljih, prihvatljiva.

Zadatak 4

Prilagodite funkciju \(f(x) = a x\) donjim podacima. Odredite parametar \(a\) i njegovu grešku te ocijenite dobrotu fita.

sage: xs2, ys2, errs2 = [range(2,25,2), [5.3,14.4,20.7,30.1,35.0,41.3,52.7,
....:                 55.7,63.0,72.1,80.5,87.9], [1.5 for k in range(2,25,2)]]
sage: errdata2 = zip(xs2, ys2, errs2)

6.2. Funkcionalno programiranje

Isti matematički problem je često moguće riješiti na različite načine, putem algoritama iza kojih stoje sasvim različiti načini razmišljanja. Razložimo to na primjeru funkcije faktorijel.

sage: factorial(7)
5040

Klasični način programiranja, upotrebljavan od dana prvih računala, je tzv. proceduralno (ili imperativno) programiranje kod kojeg na program gledamo kao na niz naredbi koje obično postupno mijenjaju vrijednosti nekih varijabli pohranjenih u memoriji računala:

sage: def factorialProc(n):
....:     fac = 1
....:     i = 1
....:     while i<n:
....:         i = i + 1
....:         fac = fac * i
....:     return fac
sage: factorialProc(7)
5040

Ovdje je očito riječ o standardnom algoritmu kakvog bismo isprogramirali u bilo kojem proceduralnom jeziku poput Fortrana ili C-a: Imamo petlju koja se prolazi n puta i svaki puta množimo rezultat prošlog prolaza sa za 1 većim brojem.

Međutim, postoje i drugačiji pristupi. Tako je kod funkcionalnog programiranja naglasak na izvrijednjavanju funkcija tj. primjeni funkcija na izraze. Faktorijel prirodno zamišljamo kao funkciju koja daje “umnožak svih brojeva od 1 do zadanog broja”.

Kao prvo, treba nam modul operator koji implementira funkcije koje odgovaraju standardnim matematičkim operacijama *, +, -,...

sage: import operator
sage: (operator.mul(2,3), operator.add(2,3))
(6, 5)

Zatim koristimo funkciju reduce(), koja kumulativno primjenjuje prvi argument (koji mora biti funkcija) na elemente drugog argumenta:

sage: f = function('f')
sage: reduce(f, range(1,5))
f(f(f(1, 2), 3), 4)

sage: reduce(operator.mul, range(1,8))
5040

Primijetite da nam ovdje nisu trebale pomoćne varijable (poput i i fac iz factorialProc), ali nam je trebalo više memorije jer smo trebali pohraniti čitavu listu [1, 2, ...] koju daje range().

Funkcionalno programiranje je stil programiranja koji stavlja naglasak na izvrijednjavanje izraza, a ne na sukcesivno izvršavanje komandi. Kod čistih funkcionalnih programa obično nema pomoćnih varijabli i nepotrebnih popratnih efekata izvrijednjavanja funkcija. U tom smislu funkcionalno programiranje je pomalo slično radu s tabličnim kalkulatorom (npr. MS Excel): redosljed izračunavanja ćelija je nebitan tj. očekujemo automatsku konzistenciju. Isto, vrijednosti ćelija su dane izrazima, a ne slijedovima komandi. (Misli se na Excel, a ne Sage ćelije.)

(Više informacija o funkcionalnom programiranju nudi Functional Programming FAQ ili WWW stranice Haskell funkcionalnog jezika.)

Takav stil programiranja često rabi nekoliko specijalnih funkcija (mogli bismo ih zvati “meta-funkcije”) čija je uloga upravljanje primjenivanjem drugih funkcija koje dolaze kao argumenti ovih meta-funkcija. Možda najvažnija takva funkcija je map() koja distribuira (mapira) funkciju po elementima neke liste:

sage: f = function('f')
sage: map(f, range(4))
[f(0), f(1), f(2), f(3)]

Ukoliko funkcija prima više argumenata, može se mapirati na više listi:

sage: map(f, range(4), range(3,7))
[f(0, 3), f(1, 4), f(2, 5), f(3, 6)]

Recimo da sad želimo ispisati tablicu s nizom prirodnih brojeva i njihovih faktorijela. Možemo prvo postupiti tako da prvo definiramo pomoćnu funkciju koja generira jedan red tablice i onda je pomoću map() primijenimo na niz brojeva:

sage: def auxfun(k):
....:     return (k, factorial(k))

sage: map(auxfun, range(7))
[(0, 1), (1, 1), (2, 2), (3, 6), (4, 24), (5, 120), (6, 720)]

Međutim, baš kao i pomoćne varijable, tako ni pomoćne funkcije nisu u duhu funkcionalnog programiranja. Zato postoje tzv. lambda-funkcije koje su bezimene i definiraju se i upotrebljavaju na slijedeći način:

sage: map(lambda k: (k, factorial(k)), range(7))
[(0, 1), (1, 1), (2, 2), (3, 6), (4, 24), (5, 120), (6, 720)]

sage: matrix(_)  # čitljiviji ispis bez uptrebe formatirajućih stringova
[  0   1]
[  1   1]
[  2   2]
[  3   6]
[  4  24]
[  5 120]
[  6 720]

Treba uočiti kako je često upotrebu funkcije map() i lambda-funkcija moguće izbjeći korištenjem obuhvaćanja liste. Npr, gornji primjer se elegantnije realizira ovako:

sage: [(k, factorial(k)) for k in range(7)]
[(0, 1), (1, 1), (2, 2), (3, 6), (4, 24), (5, 120), (6, 720)]

Kako su Sage/Python funkcije punopravni objekti, možemo i sami definirati funkcije koje primaju druge funkcije kao argumente. Evo funkcije koja implementira kompoziciju funkcija:

sage: def compose(f, n, x):
....:     """Uzastopno komponiranje funkcije sa samom sobom n puta."""
....:     if n <= 0:
....:         return x
....:     x = f(x)
....:     for i in range(n-1):
....:         x = f(x)
....:     return x

Npr. tzv. zlatni omjer \((\sqrt{5}+1)/2\) se može izraziti kao beskonačni razlomak

\[\frac{\sqrt{5}+1}{2} = 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{\cdots}}}} = 1.618034\ldots\]

Takav razlomak možemo izvrijedniti na slijedeći način:

sage: gr = compose(lambda x: 1+1/x, 5, x); gr
1/(1/(1/(1/(1/x + 1) + 1) + 1) + 1) + 1

sage: gr.subs(x=1).n()
1.62500000000000

Ili, uz povećanje točnosti:

sage: numerical_approx((1+sqrt(5))/2)
1.61803398874989
sage: compose(lambda x: 1+1/x, 32, x).subs(x=1).n()
1.61803398874986

6.2.1. Primjer razvoja funkcionalnog programa

Promotrimo razvoj programa koji ispisuje tablicu frekvencija pojavljivanja elemenata u listi. Načinimo prvo jednostavnu testnu listu

sage: lst = ['a', 'c','b', 'a', 'c', 'a', 'd', 'b', 'c','d', 'c']

Metoda liste koja daje broj pojavljivanja nekog elementa je count()

sage: lst.count('c')
4

Da bismo ispisivali tablicu trebamo listu oblika [(element1, frekvencija elementa1), (element2, frekvencija elementa2),...]. Element te liste (red tablice) se može dobiti ovako:

sage: def el(x):
....:     return (x, lst.count(x))
sage: el('c')
('c', 4)

Tablicu frekvencija za različite elemente dobijemo korištenjem lambda-funkcije analogne el() i njenom primjenom pomoću funkcije map() na popis elemenata:

sage: map(el, ['a', 'b', 'c', 'd'])
[('a', 3), ('b', 2), ('c', 4), ('d', 2)]

sage: map(lambda x: (x, lst.count(x)), ['a', 'b', 'c', 'd'])
[('a', 3), ('b', 2), ('c', 4), ('d', 2)]

To je sad to, jedino još želimo izbjeći da sami moramo ručno identificirati koji se sve elementi pojavljuju u listi. To nam može raditi funkcija uniq() koja izbacuje duplikate iz liste:

sage: res = map(lambda x: (x, lst.count(x)), uniq(lst)); res
[('a', 3), ('b', 2), ('c', 4), ('d', 2)]

Kao zadnju stvar, poželjno je listu sortirati po frekvencijama. Funkcija sorted() je već definirana tako da zna sortirati liste različitih objekata, no ovdje bi po defaultu sortirala parove po prvom elementu i to po abecednom redu, ...

sage: sorted(res)
[('a', 3), ('b', 2), ('c', 4), ('d', 2)]

... dok nama treba sortiranje po drugom elementu i to po veličini. Stoga moramo putem opcionalnog argumenta key funkciji sorted() proslijediti funkciju koja će vraćati onaj dio elementa liste po kojem želimo sortiranje:

sage: def keyfun(item):
....:     """Return last element of item."""
....:     return item[-1]

sage: sorted(res, key=keyfun, reverse=True)
[('c', 4), ('a', 3), ('b', 2), ('d', 2)]

(Opcionalni argument reverse daje silazno sortiranje umjesto defaultnog uzlaznog.)

Naravno, i ovu pomoćnu funkciju keyfun() možemo zamijeniti lambda funkcijom:

sage: sorted(res, key=lambda it: it[-1], reverse=True)
[('c', 4), ('a', 3), ('b', 2), ('d', 2)]

I to je to. Sad definiramo kompletnu funkciju:

sage: def frequencies(lst):
....:     """Elements of list lst with their frequencies."""
....:     return sorted(map(lambda x: (x, lst.count(x)), set(lst)),
....:            key=lambda it: it[-1], reverse=True)

sage: for it in frequencies(lst):
....:     print "%s: %d" % it
c: 4
a: 3
b: 2
d: 2

Primijenimo to na frekvenciju pojavljivanja slova u Shakespeareovom Mletačkom trgovcu (zapravo koristimo engleski original The Merchant of Venice, sa WWW stranica projekta Gutenberg)

sage: import urllib
sage: venice = urllib.urlopen(
....:   'http://www.gutenberg.org/ebooks/2243.txt.utf-8').read()[16400:]

sage: len(venice)
120784

sage: print venice[:370]
The Merchant of Venice

Actus primus.

Enter Anthonio, Salarino, and Salanio.

  Anthonio. In sooth I know not why I am so sad,
It wearies me: you say it wearies you;
But how I caught it, found it, or came by it,
What stuffe 'tis made of, whereof it is borne,
I am to learne: and such a Want-wit sadnesse makes of
mee,
That I haue much ado to know my selfe

sage: for it in frequencies(venice)[:10]:
....:     print "%s:  %d" % it
 :  20927
e:  12250
o:  7260
t:  7227
a:  6233
h:  5560
n:  5518
s:  5317
r:  5232
i:  5206

Vidimo da je “e” daleko najčešće slovo (poslije razmaka), činjenica vrlo važna pri dešifriranju engleskih tekstova.

Kao netrivijalniji primjer upotrebe gore definirane funkcije compose() možemo nacrtati tzv. Mandelbrotov skup, definiran kao skup svih točaka \(c\) kompleksne ravnine za koje iteracija

\[z_0 = 0\;; \qquad z_{n+1} = z_{n}^2 + c\]

ne divergira.

sage: complex_plot(compose(lambda z: z^2+x, 8, x), (-2, 1), (-1, 1))

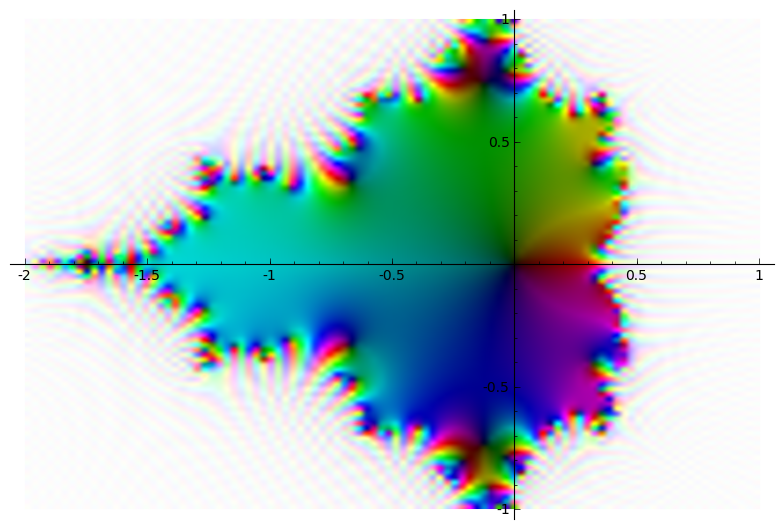
(Analizirajte sami kako radi ovaj “program”.)

Zadatak 1

Definirajte funkciju allequal() koja testira da li su svi elementi neke liste jednaki i iskoristite je da pronađete neprekidni niz od 6 istih znamenki u prvih 1000 decimala broja \(\pi\). (Za pretvaranje broja u listu znamenaka možete iskoristiti funkciju str().) Koristite ili obuhvaćanje liste ili map() tj. nije dopušteno korištenje petlji osim eventualno unutar funkcije allequal(), gdje to isto nije nužno (Naputak: all()).

Zadatak 2

Logističko preslikavanje je dano iteracijskom formulom \(x_{n+1}= \lambda x_n(1-x_n)\). Za male vrijednosti parametra \(\lambda\), to preslikavanje za veliki \(n\) konvergira k jednoj vrijednosti. Kad \(\lambda\) raste, negdje blizu \(\lambda=3\), dolazi do bifurkacije i iteracije više ne konvergiraju već skaču između dvije vrijednosti. S daljnjim rastom \(\lambda\) dolazi do nove bifurkacije i sustav se za veliki \(n\) ponavlja s periodom četiri, itd. Rezultat se može prikazati kao tzv. Feigenbaumov bifurkacijski dijagram (vidi sliku). Nacrtajte ga tako da prvo definirate funkciju composelist() koja je analogna gornjoj funkciji compose(), ali ne vraća samo kranji rezultat kompozicije funkcija već i listu sa svim međukoracima. Nakon toga iskoristite tu funkciju za iteriranje logističkog preslikavanja. Eliminirajte prvi dio liste (dok se iteracije ne stabiliziraju) i nacrtajte drugi dio pomoću list_plot(...., pointsize=1). Uočite da svaka vrijednost apscise lambda traži posebno iteriranje.

Zadatak 3

Odredite najmanji prirodni broj koji se ne može dobiti iz brojeva 2, 3, 4 i 5 korištenjem operacija zbrajanja, oduzimanja i množenja, a gdje se svaki broj smije koristiti najviše jednom. (Npr. 1=3-2, 2=3-5+4, ..., 6=2*3, ..., 14=4*5-3*2, ..., 30=(2+4)*5, .... Naputak: Od koristi se možda može pokazati već ranije korišteni modul operator, te funkcije permutations() i combinations.

Zadatak 4

Prim-brojevi blizanci su parovi prim-brojeva koji se razlikuju za dva, poput (3,5) ili (17,19). V. Brun je 1919. dokazao da suma recipročnih vrijednosti prim-brojeva blizanaca konvergira

\[B=\left(\frac{1}{3}+\frac{1}{5}\right) + \left(\frac{1}{5}+\frac{1}{7}\right) + \left(\frac{1}{11}+\frac{1}{13}\right) + \left(\frac{1}{17}+\frac{1}{19}\right) + \cdots = 1.902160583104\]

Ovako preciznu vrijednost je vrlo teško dobiti, no napišite funkciju brun(n) koja izračunava \(B\) koristeći listu od prvih n prim-brojeva. Pokušajte je isprogramirati i unutar paradigme funkcionalnog i unutar proceduralnog programiranja. Inače, zanimljivo je da je upravo računalno određivanje ove konstante ukazalo na bug u prvoj generaciji Pentium procesora.

Literatura

• Functional programming for Mathematicians
• Opsežniji tekst koji i kritizira upotrebu funkcionalnog programiranja u pythonu.
• Eseji Paula Grahama (oni koji se tiču programiranja)