5.4. Kvantna fizika¶
5.4.1. Pravokutna potencijalna jama¶
Donji kod je napravljen za Sage sustav. Možete ga izvršiti ako instalirate Sage ili online na sagemathcloud-u. Dobra je vježba konvertirati to u Jupyter/Python.
Isprogramirat ćemo funkciju koja računa kvantnomehaničke valne funkcije i pripadajuće energije vezanih stanja čestice mase \(m\) u pravokutnoj potencijalnoj jami dubine \(V\) i širine \(L\). Koristimo oznake s Wikipedijine stranice.
sage: var('a k m L V E A B G H')
(a, k, m, L, V, E, A, B, G, H)
sage: import scipy.linalg as la
sage: import numpy as np
sage: import functools
Definiramo valnu funkciju za potencijalnu jamu širine \(L\).
sage: # components of piecewise wave function
sage: psi1(G, a, x) = G*exp(a*x)
sage: psi2(A, B, k, x) = A*sin(k*x) + B*cos(k*x)
sage: psi3(H, a, x) = H*exp(-a*x)
sage: # and a complete wave function
sage: def psi(x, coefs=(0,0,0,0), wns=(0, 0), L=1, norm=1, shift=0):
....: """ coefs = (A, B, G, H)
....: wns = (k, a)
....: """
....: if x < -L/2:
....: psi = psi1(coefs[2], wns[1], x)
....: elif x > L/2:
....: psi = psi3(coefs[3], wns[1], x)
....: else:
....: psi = psi2(coefs[0], coefs[1], wns[0], x)
....: return norm*psi + shift
Valni brojevi u unutrašnjosti \(k\) i izvan jame \(a\).
sage: # hbar=1
sage: wns = {k: sqrt(2*m*E), a: sqrt(2*m*(V-E))}
Rubni uvjeti na lijevom i desnom rubu jame su da tamo valna funkcija i njena prva derivacija budu neprekidne.
sage: boundary_conditions = [
....: psi1(G, a, -L/2) == psi2(A, B, k, -L/2),
....: psi3(H, a, L/2) == psi2(A, B, k, L/2),
....: diff(psi1(G, a, x), x).subs(x=-L/2) == diff(psi2(A, B, k, x),
....: x).subs(x=-L/2),
....: diff(psi3(H, a, x), x).subs(x= L/2) == diff(psi2(A, B, k, x),
....: x).subs(x= L/2)
....: ]
Ovi rubni uvjeti predstavljaju homogeni linearni sustav jednadžbi s nepoznanicama A, B, G i H. Energije vezanih stanja su određene zahtjevom da taj sustav ima rješenje. Konkretno, pretvorit ćemo rubne uvjete u matričnu jednadžbu oblika
a energije su onda dane kao rješenja obične jednadžbe \(\det M = 0\). Zbog trenutnog buga u Sageovoj rutini za determinantu matrica 4x4 i većih (trebao bi biti ispravljen u nadolazećoj verziji Sagea) definiramo svoju rutinu za izračun determinante:
sage: def mydet(m):
....: "Evaluates determinant of 4x4 matrix m. (Sage's det() has a bug.)"
....: d = 0
....: for c in range(4):
....: ci = range(4)
....: ci.pop(c)
....: sub = m.matrix_from_rows_and_columns([1,2,3], ci)
....: d += (-1)^(c) * m[0,c] * det(sub)
....: return d
Elemente matrice \(M\) dobivamo metodom simboličkog izraza coef(), a
jednadžbu \(\det M = 0\) rješavamo algoritmom u kojem krečemo od liste
intervala [(0,V)], koja sadrži u početku samo jedan interval (0, V) i postupamo
ovako:
- Maknemo prvi interval
(a, b)iz liste (metodapop()) i tražimo u njemu nultočku. To može imati dva ishoda
- Našli smo nultočku (taj ishod je zagarantiran u prvom koraku jer jedno vezano stanje uvijek postoji). Zapišemo nađenu energiju, a listu intervala nadopunimo s dva nova intervala:
(a, E)i(E, b).- Nismo našli nultočku. Ne radimo ništa (interval je već maknut s popisa).
- Ponavljamo postupak iz točke 1. dok ne iscrpimo sve intervale. (Radi jednoznačnosti, svi intervali gore su u samom kodu zapravo za malu vrijednost
epsudaljeni od navedenih rubova.)
sage: def energies(system = {m: 1/2, L: 1, V: 25}, eps=1e-3):
....: bcs = [c.subs(wns).subs(system) for c in boundary_conditions]
....: # Preparing linear system M*coefs = 0
....: M = matrix([[(eq.lhs()-eq.rhs()).coefficient(v) for v in (A,B,G,H)]
....: for eq in bcs])
....: dt = mydet(M)
....: res = []
....: # Energies of bound states are all solutions of det(M) = 0
....: ints = [(eps, system[V]-eps)]
....: while ints:
....: int = ints.pop(0)
....: try:
....: e = find_root(dt, int[0], int[1])
....: res.append(e)
....: ints.extend([(int[0], e-eps), (e+eps, int[1])])
....: except:
....: pass
....: res.sort()
....: return res
Za provjeru odredit ćemo energije i odgovarajuće vrijednosti bezdimenzionalne varijable \(v=kL/2\) za slučaj sa spomenute stranice na Wikipediji:
sage: ens = energies(system = {m: 1/2, L: 1, V: 80}); ens
[6.557920590133058, 25.767519828716722, 55.56613192980969]
sage: # compare with wikipedia values = 1.28, 2.54, 3.73
sage: [(k*L/2).subs(wns).subs({m: 1/2, L: 1, V: 80}).subs(E=en).n()
....: for en in ens]
[1.28042186311124, 2.53808588451596, 3.72713468799458]
Sada definiramo funkciju koja za datu energiju određuje koeficijente valnih funkcija A, B, G, H. Sustav jednadžbi rubnih uvjeta nije dovoljno određen (\(\det M = 0\)!). Dodatni uvjet koji bi potpuno odredio sustav je uvjet normalizacije valnih funkcija (integral gustoće vjerojatnosti \(|\psi(x)|^2\) po cijelom prostoru mora biti jedan), ali dodavanje tog uvjeta bi učinilo jednadžbe nelinearnima pa ćemo raditi na način da privremeno fiksiramo normalizaciju valne funkcije uvjetom \(\psi(L//2)=1\), što nam fiksira vrijednost koeficijenta H i onda za preostale koeficijente rješavamo nehomogenu linearnu matričnu jednadžbu
sage: def coefs(en, system = {m: 1/2, L: 1, V: 25}):
....: """Returns (A, B, G, H) for given energy."""
....: # Fixing H by normalization psi(L/2)=1
....: hval = numerical_approx(exp(a*L/2).subs(wns).subs(system).subs(
....: {E: en}))
....: bcred = [c.subs(H=hval).subs(wns).subs(system).subs({E: en})
....: for c in boundary_conditions]
....: # Preparing linear system Mred * coefs[:-1] - Fred = 0
....: Mred = matrix([[(eq.lhs()-eq.rhs()).coeff(v) for v in (A,B,G)]
....: for eq in bcred])
....: Fred = vector([(eq.lhs()-eq.rhs()).subs({A:0, B:0, G:0})
....: for eq in bcred])
....: cfs = la.lstsq(Mred, -Fred)[0].tolist()
....: cfs.append(hval)
....: return tuple(cfs)
Sada definiramo funkciju koja kombinira gornje funkcije, normalizira dobivene
valne funkcije i vraća listu [( \(E_1\), \(\psi_1\)), ( \(E_2\),
\(\psi_2\)), ...] gdje su \(\psi_i(x)\) funkcije jednog argumenta
(\(x\)) dobivene parcijalnim izvrijednjavanjem (cf. currying ) na početku
definirane funkcije psi za različite vrijednosti njenih opcionalnih argumenata,
pomoću modula functools. (Normalizirane funkcije još množimo factorom scale
radi čitlijvijeg crtanja.)
sage: def sqwell(system = {m: 1/2, L: 1, V: 25}, scale=5.):
....: ens = energies(system)
....: print "Energies = %s" % str(ens)
....: res = []
....: for en in ens:
....: cfs = coefs(en, system)
....: #print cfs
....: norm = 1/sqrt(numerical_integral(lambda x: psi(x, cfs,
....: (k.subs(wns).subs(system).subs(E=en), a.subs(wns).subs(
....: system).subs(E=en)), L=1)**2, (-oo, oo))[0])
....: #print en,
....: fun = functools.partial(psi, coefs=cfs,
....: wns=(k.subs(wns).subs({m: 1/2, L: 1, V: 25}).subs(E=en),
....: a.subs(wns).subs(system).subs(E=en)),
....: L=system[L], norm=norm*scale)
....: #print fun(0)
....: res.append((en, fun))
....: return res
sage: def square_well(system = {m: 1/2, L: 1, V: 25}, span=2, scale=5.):
....: """span = horizontal span of figure in widhts of well
....: scale = scaling factor for wavefunctions for visibility
....: """
....: colors = ['indigo', 'firebrick', 'darkolivegreen', 'plum']
....: sol = sqwell(system)
....: P = line([[-span*system[L]/2, system[V]], [-system[L]/2,
....: system[V]], [-system[L]/2, 0],
....: [system[L]/2, 0], [system[L]/2, system[V]],
....: [span*system[L]/2, system[V]]],
....: color='darkslategray', thickness=10, alpha=0.3)
....: for (en, fun), k in zip(sol,range(len(sol))):
....: P += line([[-span*system[L]/2, en], [span*system[L]/2, en]],
....: color=colors[k], thickness=0.4)
....: P += plot(lambda x: fun(x, shift=en), (-span*system[L]/2,
....: +span*system[L]/2), color=colors[k])
....: P.show()
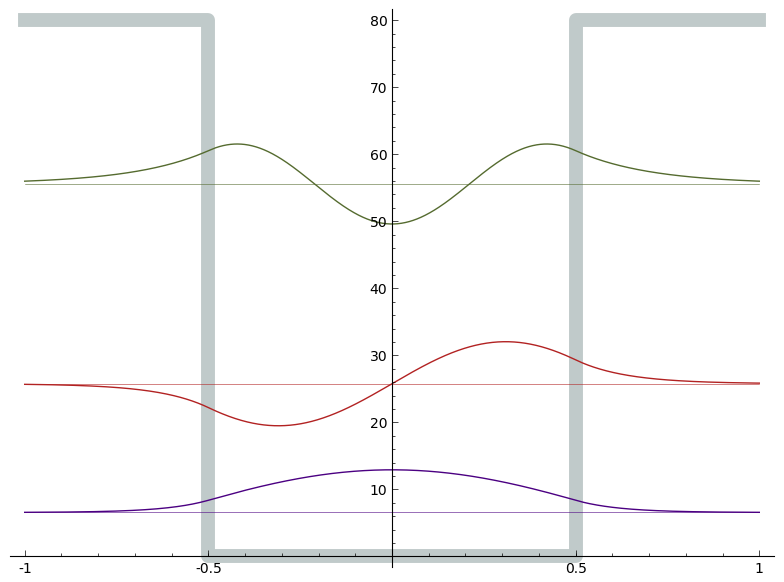
sage: square_well(system = {m: 1/2, L: 1, V: 80})
Energies = [6.557920590133058, 25.767519828716722, 55.56613192980968]