Vrtnja kotača



Padne li nam pogled na kotač koji se vrti – recimo, na motociklu u vožnji – s vremena na vrijeme nam se može učiniti kao da se vrti "unatrag", u smjeru suprotnom od onoga u kojem bi trebao da bi se motocikl kretao unaprijed. Poznato je da je tom prividu uzrok tromost oka, stoga ćemo proučiti na koji način doista dolazi do tog fenomena.

Oko, poput svakog optičkog uređaja, ima ograničenu vremensku razlučivost u procesu sabiranja slike. Tako je opće poznato da su pri projiciranju filmova dovoljne 24 sličice u sekundi da bi se oko uvjerilo u kontinuirani razvoj slike. Prema tome, baš poput kamere, oko neprestano periodički okida te ne može raspoznati detalje u razvoju slike između tih bljeskova. Označimo s T vremenski interval između dvaju uzastopnih okidanja oka, koji ugrubo možemo procijeniti upravo na T = 1/24 s.

A sada promotrimo što se događa s kotačem u vrtnji. Kotač koji se u vremenskom intervalu Δt zakrene za kut Δφ, vrti se kutnom brzinom ω jednakom:



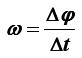
No, ako je period okidanja oka T, ono ne može raspoznati zakret kotača koji s odvio unutar vremena manjeg od T. Prema tome, najmanji kut zakreta φT koji oko može prepoznati jednak je:



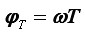
Uzmimo radi jednostavnosti da kotač ima samo jedan krak kojim su njegov centar i obod povezani. Kasnije ćemo rezultat poopćiti na realističan kotač s više (proizvoljno mnogo) zvjezdasto raspoređenih krakova. Neka se pri tome kotač vrti u smjeru suprotnom od kazaljke na satu te je za početak vrtnja toliko spora da se unutar jednog perioda oka zakrene za manje od pola kruga, tj. 0 < φT < π. Na Slici 1 prikazan je razvoj slike koji oko registrira uzastopnim okidanjem u pravilno raspoređenim vremenskim trenucima.



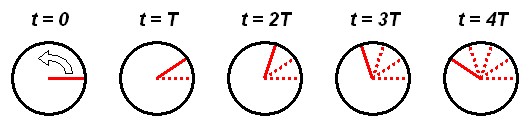
Slika 1 – Privid vrtnje kotača za 0 < φT < π


Primjećujemo da oko vidi da se kotač vrti u ispravnom smjeru, i to brzinom kojom se doista vrti. Prema tome, ako s ωeff označimo efektivnu kutnu brzinu kotača – prividnu brzinu, onu koju oko vidi – u ovom slučaju vrijedi:



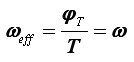
No, što se događa ako se kotač vrti brže, toliko da unutar vremena T prebriše više od pola kruga, tako da je π < φT < 2π? Na Slici 2 situacija je prikazana za brzinu toliku da se kotač okrene gotovo za puni krug unutar perioda između dvaju okidanja oka.



Slika 2 – Privid vrtnje kotača za π < φT < 2π


Ovaj put nam se čini da se kotač vrti u suprotnom smjeru! I to upravo zbog tromosti oka, jer ono ne može razlučiti što se događalo između njegovih dvaju okidanja! No, kako se to odražava na prividnu brzinu vrtnje kotača? Oko ne može znati da je kotač napravio gotovo puni krug, zakret za φT. Ono zna jedino ono što vidi, a to što vidi interpretira na najjednostavniji mogući način, koji u ovome slučaju odgovara tome da je kotač napravio manji zakret u suprotnom smjeru, pri čemu je prividno prebrisao efektivni kut φeff, koji je stvarni okret umanjen za puni krug (2π):



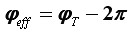
Kako je φT < 2π, slijedi da je φeff < 0, što upravo odražava činjenicu da je prividni zakret bio unatrag, u smjeru suprotnom od ispravnoga za koji vrijedi φT >0. Dakle, prividna brzina vrtnje kotača ovoga puta jednaka je:



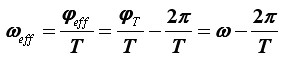
pri čemu je, podsjetimo se, ω stvarna kutna brzina kotača. Kako je φeff < 0, tako je i ωeff < 0, a to je upravo rezultat koji opisuje prividnu vrtnju unatrag.

Ali nemojmo se zaustaviti ovdje. Neka se kotač vrti još brže, toliko da unutar T napravi više od jednog punog kruga, ali manje od kruga i pol, tj.: 2π < φT < 3π. Ono što oko ovaj put vidi jednako je početnom slučaju, prikazanom na Slici 1, no ovaj put oko ne zna da je kotač između dvaju okidanja stigao napraviti puni krug, pa upravo kao i u prvom slučaju vidi pomak za mali kut unaprijed, koji je pravi kut zakreta umanjen za taj "izgubljeni" puni krug:



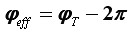
Primjetimo da je, iako oko vidi istu sliku kao u prvom slučaju, izraz koji opisuje φeff jednak onome iz drugog slučaja. No, ovoga puta je φeff > 0, što upravo znači da oko ponovno vidi vrtnju unaprijed. Prema tome, prividna brzina jednaka je prethodnom slučaju:



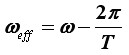
i iako je ovoga puta ispravnog predznaka (ωeff >0), očito nije ispravnoga iznosa. Dakle, ovoga puta oko vidi da se kotač vrti u ispravnom smjeru, no brzinom manjom od prave.

Ubrzavajmo kotač i dalje, tako da je ovoga puta 3π < φT < 4π, tj. prebrisani kut unutar T je između punog i pol te dva puna kruga. U ovom slučaju oko je više zavarano nego ikada prije. Naime, ne samo da ne zna da je kotač uspio napraviti više od punog kruga kao i u prethodnom slučaju, već mu se kao i u drugom slučaju čini da se okrenuo za manji kut unatrag, umjesto za veći kut unaprijed. Prema tome, prividni kut zakreta jednak je:



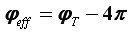
pri čemu je prvih 2π oduzeto zbog izgubljenog punog okreta, a slijedećih 2π zbog toga jer se prebrisani kut našao bliže slijedećem punom krugu nego prethodnom, već upotpunjenom. Odmah zaključujemo:



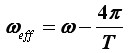
I baš kao u drugom slučaju, φeff i ωeff su ponovno negativni, dakle privid vrtnje je opet pogrešnoga smjera, a ωeff je pogrešnoga iznosa te oko nema načina zaključiti kolika je ispravna kutna brzina ω kotača (osim, eventualno, na temelju zamućenja slike jer je za manje ω slika jasnija i suprotno.).

Uz daljnje povećanje obodne brzine kotača, tako da je 4π < φT < 5π, oko će ponovno vidjeti vrtnju u pravom smjeru, no između svaka dva okidaja izgubit će dva puna kruga koja je kotač već stigao odvrtiti. Stoga ponovno vrijedi:




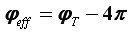
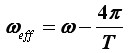
Nadalje, za 5π < φT < 6π, uz gubitak dva puna kruga po svakom periodu, ponovno se javlja privid obrnute vrtnje uz negativne vrijednosti φeff i ωeff:




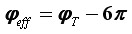
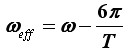
I tako dalje, sve brže i brže...

Sada već možemo primjetiti određenu pravilnost koja se javlja. Naime, oko izgubi svaki puni krug koji kotač prevali unutar jednog perioda T (dakle, N punih krugova povlači smanjenje prividnog kuta za 2Nπ s obzirom na puni prebrisani: φeff = φT – 2Nπ). A ako je još nakon toga ostatak i veći od pola punog kruga, oduzima je još jedan dodatan faktor od 2π (pa je u tom slučaju: φeff = φT – 2(N+1)π).

Matematički malo preciznije iskazano, ako je za {nπ < φT < (n+1)π} n paran, tada je:



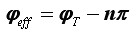
dok je za neparan n:



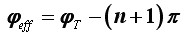
Drugim riječima, uz π u prethodnom izrazu od faktora n ili n+1 dolazi onaj koji je paran.

I napokon, uz tu vezu utvrđenu, možemo zapisati konačno rješenje za prividnu brzinu vrtnje kotača u ovisnosti o njegovoj stvarnoj brzini te parametrima oka. Dakle, iz:



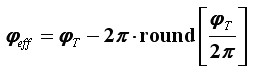
slijedi traženi eksplicitni izraz:



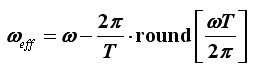
Pri tome round[x] označava najbliži cijeli broj od x (jednostavna funkcija "zaokruživanja") te je vrlo lako uvjeriti se da funkcija round[ ] reproducira uočenu pravilnost u φeff, odnosno ωeff.

Sve što još želimo je poopćiti rezultat na kotač s više od jednog kraka, i to proizvoljno mnogo njih, a to poopćenje provodimo vrlo jednostavno. Naime, kotač s jednim krakom vratio se u početni položaj najranije nakon prebrisanog punog kruga pa je kut s obzirom na koji smo promatrali vrtnju bio 2π. Ali kotač s K simetrično raspoređenih krakova izgledat će isto kao u početnom trenutku i već kad prebriše K-ti dio punog kruga! Prema tome, referentni kut postaje 2π/K te je u konačom rješenju samo potrebno provesti zamjenu svih članova 2π s 2π/K, nakon čega preostaje:



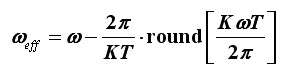
Općenit oblik rješenja za ωeff prikazan je na Grafu 1.



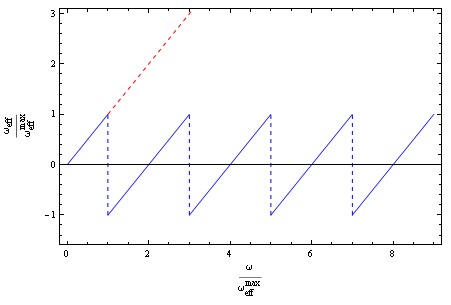
Graf 1 – Prikaz rješenja za prividnu kutnu brzinu kotača (plava linija) u ovisnosti o njegovoj stvarnoj brzini (koja je, osim na osi, dodatno prikazana i crvenom crtkanom linijom)


Na rastućim dijelovima grafa jasno se može vidjeti prelazak ωeff preko nule (za vrijednosti 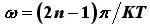uz n kao prirodan broj), pri čemu brzina vrtnje kontinuirano (!) mijenja predznak, odnosno smjer. Pri tome je naglasak na kontinuiranosti promjene jer vrtnja kotača u suprotnom smjeru (područje ωeff < 0) postepeno usporava, do prividnog zaustavljanja (ωeff = 0; slučaj kada kotač unutar perioda T prebriše cijeli broj punih krugova) da bi zatim ponovno krenula ubrzavajući u ispravnom smjeru (ωeff > 0). Ovaj dio rezultata nas ne iznenađuje jer je kontinuiranost prirodno očekivati. No, ono što nas na prvi pogled zbunjuje i začuđuje su nagli skokovi između najviše i najniže vrijednosti ωeff – diskontinuiteti u vrijedostima 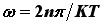(ponovno uz n kao prirodan broj) koji vode od 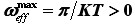do 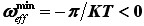. No, lako je ustanoviti porijeklo i opravdanost tih diskontinuiteta. Naime, sam model od kojega smo krenuli i kojim smo opisali funkcioniranje oka – periodičnim okidanjem – inherentno, sam po sebi sadrži i oslanja se na diskontinuiranu pojavu jer je svaki bljesak oka vrlo brz, nagao, diskretan, diskontinuiran proces. Naravno da u stvarnosti taj proces nije toliko oštar, već je doista kontinuiran, no da ta korekcija ne utječe (niti donekle značajno) na valjanost našeg rezultata, možemo se uvjeriti sa priloženog filmića. A što se tiče same provjere i potvrde vizualnog efekta filmskom snimkom, posebno prikladna okolnost je što smo na samom početku mehanizam oka usporedili i poistovjetili s mehanizmom filmske kamere. Prema tome, gledajući filmsku snimku gledamo upravo u sliku snimljenu na način kojim bi je samo oko "snimilo" i vidjelo.


Link na flimić:



Dok oko 13-te sekunde uočavamo promjenu prividnog smjera vrtnje uz usporenje iz suprotnog pa ubrzanje u ispravnom smjeru (kontinuirani prijelaz ωeff preko nule), oko 30-te sekunde doista se možemo uvjeriti u pojavu diskontinuiteta! Vidimo kako brzina vrtnje postiže svoj maksimum u jednom smjeru, nakon čega umjesto usporavanja do zastoja privid vrtnje nakratko postaje neodređen da bi se dalje nastavio u suprotnom smjeru, ali također maksimalnom brzinom. Ta trenutna promjena smjera vrtnje bez usporavanja i ubrzavanja, tj. bez promjene iznosa brzine u međuvremenu upravo je srž zanimljivog diskontinuiteta koji se pojavio.

Grafom 2 pojašnjeno je još jedno ispravno predviđanje dobivenog rezultata. Na njemu je prikazan isječak s Grafa 1 koji se odnosi na gibanje kotača prikazanom na priloženom filmiću.



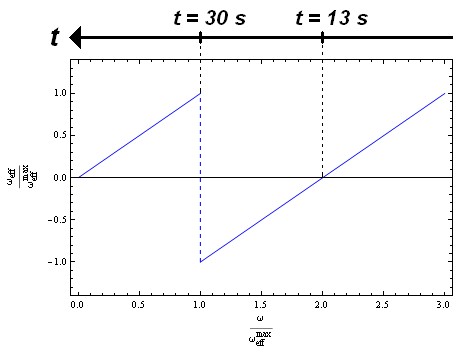
Graf 2 – Vremenski poredak događaja (referenca na priloženi filmić) ispravno predviđen dobivenim rješenjem


Kako prikazani kotač usporava (ω se smanjuje), njegova brzina se u vremenu pomiče unatrag po osi ω s Grafa 2 – prema vrijednosti ω = 0 i potpunom zaustavljanju. Lako uočavamo da dobiveni rezultat prikazan na Grafu 2 predviđa prvo kontinuirani prelazak ωeff preko nule, a zatim diskontinuirani skok prije samog zaustavljanja. Upravo u tom vremenskom poretku izmjenjuju se događaji na prikazanom filmiću: kontinuirani prijelaz ranije (13. sekunda), a diskontinuirani kasnije (30. sekunda). Time smo se uvjerili u ispravnost dobivenog rezultata s više od jednog stajališta.