 |
 |
Uvod Counter-steering Skretanje naginjanjem * |
Da bi se u vožnji motocikla skrenulo u željenome smjeru, potrebno je nagnuti motocikl, tj. pomaknuti težište motocikla i vozača u smjeru skretanja. Naginjanje se, pak, započinje (laganim) okretanjem upravljača u smjeru suprotnom od smjera skretanja (eng. counter-steering). U većini slučajeva ta metoda je toliko suptilna da je vozač svjesno niti ne primjećuje – tako je, na primjer, pri nižim brzinama gotovo potpuno prikrivena puno izraženijim i naglijim manipulacijama upravljačem kojima se ispravlja putanja i održava ravnoteža. Jednom kad je metodom counter-steeringa naginjanje započelo, vozač je može nastaviti zabacivanjem mase, ali njime nije moguće pokrenuti nagib. (Demonstracija toga se jasno može vidjeti ovdje.) Naime, kako se vozač bočno opire o motocikl da bi pomaknuo svoje težište, upravo time gura motocikl u suprotnome smjeru te pomiče i njegovo težište. Konačan rezultat je pomak pojedinih težišta vozača i motocikla, ali ne i težišta njihovog cjelokupnog sustava. To je posljedica toga što je vozač, koji djeluje silom, sâm dio sustava na koji djeluje – da bi se pomaknulo težište čitavog sustava, potrebna je neka izvanjska sila koja će mu u procesu promijeniti količinu gibanja. Zakon očuvanja količine gibanja zabranjuje da se tako nešto postigne iz sâmog sustava na koji se djeluje. Rješenje se nalazi u tome što se u sustavu vozač-motocikl kotači motocikla vrte. Kao takvi, imaju zamah, a budući da vozač nije dio sustava sâmih kotača, on svojim djelovanjem može promijeniti njihovo stanje gibanja. |
 |
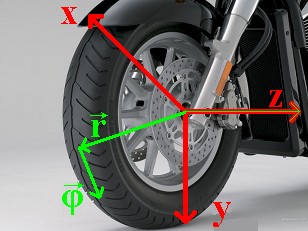 Slika 1 – Postava koordinatnog sustava na kotaču |
Kotač u vrtnji ima određeni zamah (kutnu količinu gibanja) s obzirom na svoje središte. Na Slici 1 postavljeni su pozitivno orijentirani Kartezijev (koordinate [x, y, z] ) i cilindrični (koordinate [r, φ, z] ) sustav. Dok se motocikl giba prema naprijed, obod kotača se vrti u smjeru jediničnog vektora 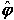 , što znači da vektor količine gibanja , što znači da vektor količine gibanja 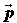 svake točke na kotaču ima upravo taj smjer. Rastavimo li za proizvoljnu točku na kotaču njen vektor količine gibanja kao: svake točke na kotaču ima upravo taj smjer. Rastavimo li za proizvoljnu točku na kotaču njen vektor količine gibanja kao: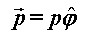 a njen radijvektor 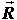 kao: kao: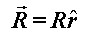 gdje su p i R iznosi (moduli) pripadnih vektora, uz definiciju zamaha 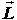 : :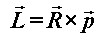 lagano se dolazi do sâmog 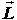 : :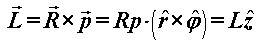 Iz toga proizlazi da smjer vektora zamaha odgovara smjeru jediničnog vektora 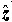 . .Dakle, giba li se motocikl prema naprijed, zamasi kotača su usmjereni "ulijevo". Na Slici 2 prikazano je kako to izgleda. |
 Slika 2 – Smjer vektora zamaha kotača dok se motocikl giba prema naprijed |
Pretpostavimo da u vožnji želimo motociklom skrenuti ulijevo. Ideja counter-steeringa je da tada treba zakrenuti upravljač udesno. |
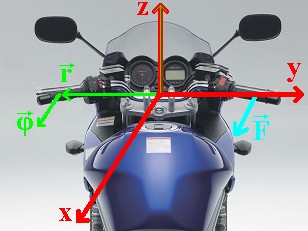 Slika 3 – Postava koordinatnog sustava na upravljaču |
Na Slici 3 postavljen je koordinatni sustav u sklopu kojega ćemo obraditi problem. U cilindričnom sustavu situacija je vektorski jednaka za obje ručke upravljača. Radijvektor ručke na koju se primjenjuje sila za skretanje dan je s: 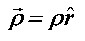 dok je sila za zakretanje upravljača udesno dana s: 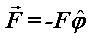 ρ i F su moduli pripadnih vektora. Pri tome se preko svake ručke stvara moment sile 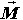 koji, izračunom po definiciji, ispada: koji, izračunom po definiciji, ispada: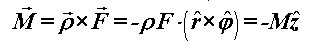 |
Primjećujemo da moment sile ima smjer negativnog jediničnog vektora 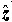 , tj. prema "dolje". Budući da je moment sile vremenska derivacija zamaha: , tj. prema "dolje". Budući da je moment sile vremenska derivacija zamaha: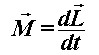 tj., prikazuje promjenu zamaha u vremenu, iz Slike 4 se jasno očitava da će zamah  dobiti komponentu u smjeru momenta sile dobiti komponentu u smjeru momenta sile  te će se pri tome zakrenuti prema "dolje". S obzirom na to da je vektor zamaha okomit na ravninu rotacije tijela (u našem slučaju kotača), proizlazi da će se upravo zakrenuti ravnina u kojoj se kotač vrti, a time i čitav motocikl. Također, primjećujemo da se u ovom slučaju ta ravnina, dakle motocikl, naginje ulijevo (rezultat koji je prikazan na Slici 5). Dok smo upravljač zakrenuli udesno. te će se pri tome zakrenuti prema "dolje". S obzirom na to da je vektor zamaha okomit na ravninu rotacije tijela (u našem slučaju kotača), proizlazi da će se upravo zakrenuti ravnina u kojoj se kotač vrti, a time i čitav motocikl. Također, primjećujemo da se u ovom slučaju ta ravnina, dakle motocikl, naginje ulijevo (rezultat koji je prikazan na Slici 5). Dok smo upravljač zakrenuli udesno. |
 Slika 4 – Moment sile koji mijenja zamah kotača |
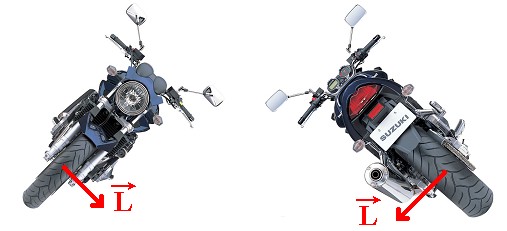 Slika 5 – Naginjanje motocikla ulijevo kao rezultat zakretanja upravljača udesno (counter-steering) |
 |
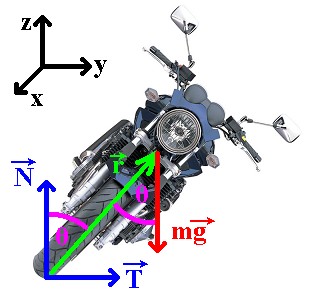 Slika 6 – Sile na motocikl uz krak sile na težinu |
Jednom kad je motocikl nagnut, razvija se moment sile uzrokovan pomakom težišta te zbog tog momenta motocikl skreće. Na Slici 6 prikazane su sile koje djeluju na skrećući motocikl u nagibu pod kutem θ. 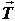 je sila trenja između gume i tla, je sila trenja između gume i tla, 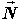 je reakcija podloge, a je reakcija podloge, a 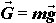 težina motocikla i vozača koja djeluje iz njihovog zajedničkog težišta. Dokle je motocikl u stalnom nagibu, ukupna reakcija podloge (reakcija na oba kotača) iznosom je jednaka težini motocikla i vozača: težina motocikla i vozača koja djeluje iz njihovog zajedničkog težišta. Dokle je motocikl u stalnom nagibu, ukupna reakcija podloge (reakcija na oba kotača) iznosom je jednaka težini motocikla i vozača: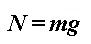 Trenje, pak, ima ulogu centripetalne sile: 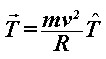 Pri tome je v brzina motocikla, R radijus kružne putanje, a 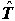 jedinični vektor u smjeru sile trenja. Uz koeficijent trenja μ između gume i tla, najveća vrijednost koju ono može postići dana je s: jedinični vektor u smjeru sile trenja. Uz koeficijent trenja μ između gume i tla, najveća vrijednost koju ono može postići dana je s: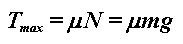 Iz toga se lagano iščitava i uvjet stabilnosti motocikla, pod kojim se motocikl u nagibu još uvijek neće prevrnuti zbog bočnog proklizavanja kotača: 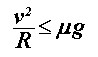 Sa slike se također lako očitava veza kuta nagiba θ i dinamičkih parametara motocikla: 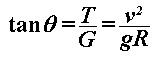 Uz tu relaciju, prethodni uvjet stabilnosti možemo dovesti u vezu sa sâmim nagibom motocikla: 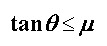 |
Postavimo Kartezijev koordinatni sustav orijentiran kao na Slici 6. Težina je sila koja je bitna i odgovorna za skretanje. Kao što se vidi na slici, radijvektor težišta, tj. krak sile (težine) je usmjeren od tla (kao čvrste podloge) prema težištu. Izrazimo vektore težine i njenog kraka: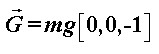 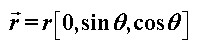 Sve što je potrebno izračunati je moment sile zbog težine: 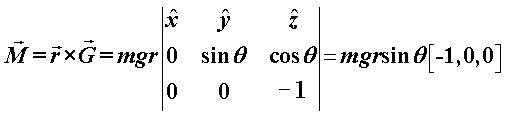 Prema tome, moment sile ima smjer suprotan od smjera kretanja motocikla, tj. prema "natrag". I ponovno, moment sile mijenja zamah kotača, i to tako da zamah dobiva komponentu u njegovom smjeru. Konačno, kako se mijenja smjer vektora zamaha, tako se zakreće ravnina vrtnje kotača, koja je okomita na taj vektor. Iz Slike 7 se jasno očitava kako će se ta ravnina zakrenuti ulijevo kada je motocikl nagnut ulijevo. |
 Slika 7 – Moment sile (težine) mijenja zamah kotača tako da motocikl skreće |
* * * |