 |
Uvod Model 1 Model 2 Model 3 |
Za vrijeme motociklističkih utrka jasno se može uočiti kako natjecatelji u svaki zavoj ulaze uz vanjski rub staze, zatim stežu svoju putanju prema apex-u koji je redovito točka na unutarnjem rubu, te konačno (ako je zavoj posljednji u nizu) iz zavoja izlaze ponovno se pomičući prema vanjskom rubu. Budući da je njihova namjera postići čim kraće prolazno vrijeme u svakome krugu, takva taktika sugerira da time biraju put najbržeg prolaska kroz zavoj. Opće je poznato da je ista strategija primjenjiva i u cestovnoj vožnji motocikla, no u tom slučaju je njena svrha sigurniji prolazak kroz krivinu na cesti, uz što manju potrebu za ekstremnim naginjanjem, a bez potrebe za pretjeranim usporavanjem. Na jednostavnom modelu zavoja konstantnog radijusa zakrivljenosti pokušat ćemo pokazati je li, zašto i pod kojim uvjetima takav pristup ulasku u zavoj opravdan. |
 |
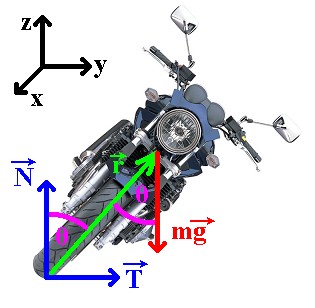 Slika 1 – Sile na motocikl u zavoju |
Na motocikl u nagibu djeluje više sila, od kojih su one ključne za našu analizu prikazane na Slici 1. 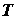 je bočna sila trenja gume na asfaltu, je bočna sila trenja gume na asfaltu, 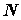 je reakcija podloge, a je reakcija podloge, a 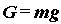 zajednička težina motocikla i vozača. Dok god motocikl ne mijenja svoj nagib, ukupna reakcija podloge je iznosom jednaka je težini zajednička težina motocikla i vozača. Dok god motocikl ne mijenja svoj nagib, ukupna reakcija podloge je iznosom jednaka je težini  : :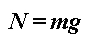 Bočno trenje djeluje kao centripetalna sila: 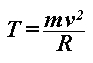 pri čemu je 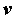 brzina motocikla, a brzina motocikla, a 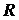 radijus njegove kružne putanje. Uz koeficijent trenja radijus njegove kružne putanje. Uz koeficijent trenja 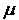 između gume i asfalta, ono je iznosom najviše: između gume i asfalta, ono je iznosom najviše: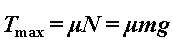 iz čega proizlazi uvjet pod kojim još neće doći do bočnog proklizavanja kotača: 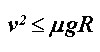 Iz slike očiglednom postaje i veza između kuta nagiba motocikla 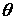 i parametara njegove putanje: i parametara njegove putanje: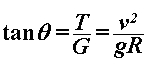 što se uz ograničenje zbog maksimalnog trenja svodi na: 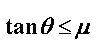 |
Pretpostavimo sada da motociklom ulazimo u zavoj oblika kružnog luka odsječenog pod kutem 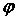 , kao što je prikazano na Slici 2, te pri tome održavamo stalan nagib, a time i radijus zakrivljenosti svoje putanje. Vrijeme potrebno za prolaz kroz sâm zavoj po liniji fiksnog radijusa , kao što je prikazano na Slici 2, te pri tome održavamo stalan nagib, a time i radijus zakrivljenosti svoje putanje. Vrijeme potrebno za prolaz kroz sâm zavoj po liniji fiksnog radijusa  je omjer prijeđenog puta (koji je duljina kružnog luka) i brzine prolaska: je omjer prijeđenog puta (koji je duljina kružnog luka) i brzine prolaska: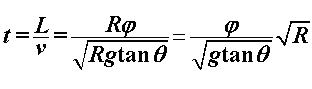 Promotrimo kako se odnose vremena prolazaka za dvije odabrane linije koje se razlikuju samo po svojim radijusima, uz izbor da je  : : Dakle, luku šireg radijusa odgovara duže vrijeme prolaska. No, u ovom slučaju nismo uzeli u obzir uvjet da se "vrh" putanje šireg radijusa mora poklopiti s unutarnjim rubom staze. Posljedica tog zahtjeva je da ulasci u zavoj po linijama različitih radijusa ne započinju na istome mjestu na stazi. |
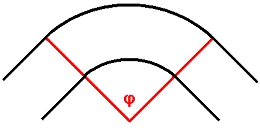 Slika 2 – Zavoj kuta φ |
 |
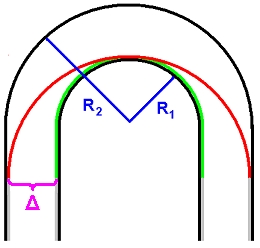 Slika 3 – Položaj šire (crvena) i uže (zelena) putanje |
Uključimo sada zahtjev da apex šire putanje mora završiti uz unutranji rub zavoja. Zor te situacije se jasno vidi na Slici 3 koja radi jednostavnosti prikazuje polukružnu putanju, ali zadržimo pretpostavku da je zavoj proizvoljnoga kuta 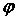 . Očito je da ulazak u zavoj po široj liniji (crvena) počinje prije, a završava dalje nego po užoj (zelena). Utvrditi koja je putanja vremenski isplativija znači odrediti za koju će vrijeme prolaska istim (!) dijelom staze biti kraće. Dakle, za liniju užeg radijusa je nužno uzeti u obzir da se sâm zavoj ne proteže čitavom njenom duljinom, već njen dio prolazi ravnim komadom staze. Iz Slike 3 je jasno da su dva takva komada – jedan prije i jedan poslije zavoja – te da su u ovakvom pojednostavljenom simetričnom modelu jednaki. Uz oznaku . Očito je da ulazak u zavoj po široj liniji (crvena) počinje prije, a završava dalje nego po užoj (zelena). Utvrditi koja je putanja vremenski isplativija znači odrediti za koju će vrijeme prolaska istim (!) dijelom staze biti kraće. Dakle, za liniju užeg radijusa je nužno uzeti u obzir da se sâm zavoj ne proteže čitavom njenom duljinom, već njen dio prolazi ravnim komadom staze. Iz Slike 3 je jasno da su dva takva komada – jedan prije i jedan poslije zavoja – te da su u ovakvom pojednostavljenom simetričnom modelu jednaki. Uz oznaku 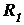 za radijus zakrivljenosti unutarnjeg ruba zavoja te za radijus zakrivljenosti unutarnjeg ruba zavoja te 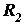 za onaj vanjskoga ruba, definiramo širinu staze za onaj vanjskoga ruba, definiramo širinu staze  kao udaljenost njenih rubova, tj. razliku danih radijusa: kao udaljenost njenih rubova, tj. razliku danih radijusa: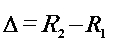 Budući da Slika 3 prikazuje polukružan zavoj ( 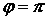 ) koji je zapravo specijalan slučaj zavoja proizvoljnoga kuta ) koji je zapravo specijalan slučaj zavoja proizvoljnoga kuta 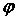 , iz nje se lako uočava da je radijus zakrivljenosti šire putanje jednak vanjskom radijusu staze ( , iz nje se lako uočava da je radijus zakrivljenosti šire putanje jednak vanjskom radijusu staze (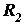 ), a pojednini ravni dio u sklopu uže putanje jednak širini staze ( ), a pojednini ravni dio u sklopu uže putanje jednak širini staze ( ). No, to ne vrijedi za općeniti ). No, to ne vrijedi za općeniti 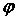 . Naime, kao što se vidi na Slici 4 i Slici 5, radijus šire putanje je općenito još veći nego radijus vanjskog ruba staze, a zbog toga se mijenja i duljina ravnog dijela uže putanje! Radijus uže putanje u svakom slučaju ostaje jednak onome unutarnjeg ruba staze. . Naime, kao što se vidi na Slici 4 i Slici 5, radijus šire putanje je općenito još veći nego radijus vanjskog ruba staze, a zbog toga se mijenja i duljina ravnog dijela uže putanje! Radijus uže putanje u svakom slučaju ostaje jednak onome unutarnjeg ruba staze. |
Prvo ćemo izračunati radijus zakrivljenosti 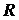 šire putanje oslanjajući se na Sliku 4. Putanja počinje i završava uz vanjski rub staze, stoga sa svake strane zavoja u točkama u kojima se ona odvaja ili spaja s vanjskim rubom možemo povući tangente na putanju (plavo) koje su paralelne s odgovarajućim ravnim dijelom staze te se sijeku u točki udaljenoj za šire putanje oslanjajući se na Sliku 4. Putanja počinje i završava uz vanjski rub staze, stoga sa svake strane zavoja u točkama u kojima se ona odvaja ili spaja s vanjskim rubom možemo povući tangente na putanju (plavo) koje su paralelne s odgovarajućim ravnim dijelom staze te se sijeku u točki udaljenoj za 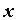 od apexa unutarnjeg ruba zavoja. Iz označenoga na Slici 4, primjenom geometrije i trigonometrije dolazimo do slijedećih dviju relacija: od apexa unutarnjeg ruba zavoja. Iz označenoga na Slici 4, primjenom geometrije i trigonometrije dolazimo do slijedećih dviju relacija: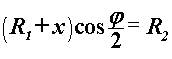 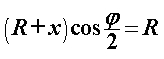 Eliminacijom nepoznanice 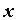 iz prethodnih jednadžbi te upotrebom trigonometrijskih identita i definicije za iz prethodnih jednadžbi te upotrebom trigonometrijskih identita i definicije za  , preostaje konačan izraz za radijus šire putanje: , preostaje konačan izraz za radijus šire putanje: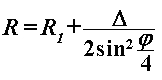 |
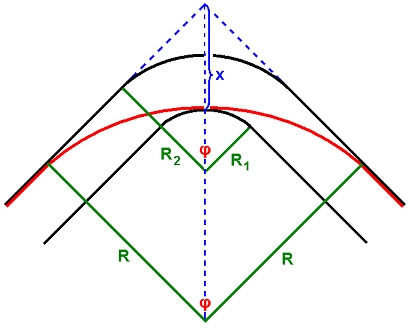 Slika 4 – Radijus zakrivljenosti šire putanje |
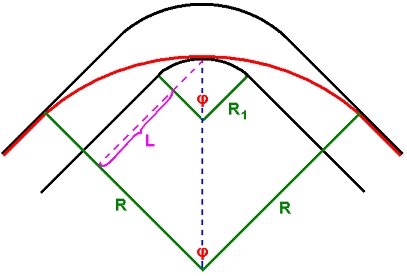 Slika 5 – Duljine ravnih dijelova uže putanje |
Još prostaje izračunati duljinu 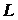 pojedinog ravnog dijela uže putanje. Iz Slike 5 se lako očitava geometrijska veza: pojedinog ravnog dijela uže putanje. Iz Slike 5 se lako očitava geometrijska veza: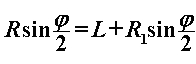 iz čega uvrštavanjem izraza za 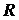 te upotrebom trigonometrijskih identiteta proizlazi: te upotrebom trigonometrijskih identiteta proizlazi: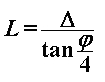 |
Vratimo se sada na pitanje za koju je putanju vrijeme prolaska kroz zavoj kraće. Zadržat ćemo temeljnu pretpostavku da kroz sâm zavoj prolazimo uz konstantnu brzinu i nagib motocikla, no ovaj put u obzir uzimamo i ravne komade uže putanje. U sklopu ovog modela ćemo promatrati kako se odnose vremena za širu i užu putanju ako ravnim dijelovima uže putanje vozimo konstantnom brzinom jednakom onoj kojom prolazimo kroz sâm zavoj. Šira putanja radijusa 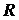 sastoji se samo od prolaska zavoja te za njeno trajanje koristimo već dobiveni rezultat iz prvog modela: sastoji se samo od prolaska zavoja te za njeno trajanje koristimo već dobiveni rezultat iz prvog modela: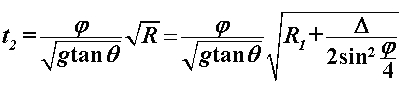 Duljina puta uže putanje radijusa 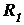 sastoji je od kružnog luka (zavoj) i dvostrukog ravnog komada, pri čemu je brzina također određena na jednak način kao u prvom modelu: sastoji je od kružnog luka (zavoj) i dvostrukog ravnog komada, pri čemu je brzina također određena na jednak način kao u prvom modelu: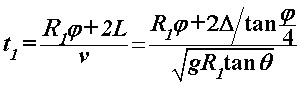 Naš cilj je pokazati da je šira putanja vremenski isplativija, dakle pokušavamo dokazati da je: 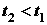 . Izravnim uvrštavanjem dobivenih rezultata nejednakost poprima oblik: . Izravnim uvrštavanjem dobivenih rezultata nejednakost poprima oblik: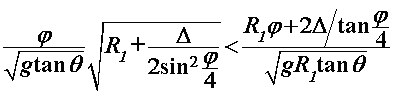 Budući da su nam vremenski intervali smisleni samo ako su pozitivni, nejednakost možemo kvadrirati sigurni da neće doći do promjene predznaka: 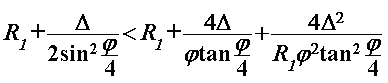  je širina staze te je također smislena jedino kao pozitivan broj pa i njime možemo dijeliti nejednakost. Kut je širina staze te je također smislena jedino kao pozitivan broj pa i njime možemo dijeliti nejednakost. Kut 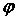 je formalno ograničen na vrijednosti s intervala od 0 do 2π (uz pretpostavku čitave staze na istoj nadmorskoj visini). Budući da je argument svih trigonometrijskih funkcija unutar nejednakosti je formalno ograničen na vrijednosti s intervala od 0 do 2π (uz pretpostavku čitave staze na istoj nadmorskoj visini). Budući da je argument svih trigonometrijskih funkcija unutar nejednakosti 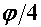 , on poprima vrijednosti od 0 do π / 2. Na tom su intervalu sve te funkcije pozitivne, stoga njima također možemo množiti nejednakost. Nakon odgovarajućeg sređivanja, ona se svodi na: , on poprima vrijednosti od 0 do π / 2. Na tom su intervalu sve te funkcije pozitivne, stoga njima također možemo množiti nejednakost. Nakon odgovarajućeg sređivanja, ona se svodi na: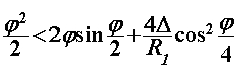 |
Područje na kojem vrijedi ova nejednakost trebali bismo ispitati u ovisnosti o kutu 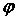 i omjeru i omjeru 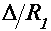 , no takvog je oblika da ju je vrlo teško egzaktnko riješiti, ako ne i nemoguće. Budući da su svi članovi u njoj pozitivni, čim više ćemo restriktirati njeno područje maksimalno joj smanjivši desnu stranu – to ćemo postići uvrštavanjem , no takvog je oblika da ju je vrlo teško egzaktnko riješiti, ako ne i nemoguće. Budući da su svi članovi u njoj pozitivni, čim više ćemo restriktirati njeno područje maksimalno joj smanjivši desnu stranu – to ćemo postići uvrštavanjem 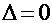 . Taj slučaj nije fizikalan, ali želimo ostvariti "najcrnji scenarij" kako bismo zaključili što sa sigurnošću vrijedi. Taj slučaj je ekvivalentan: . Taj slučaj nije fizikalan, ali želimo ostvariti "najcrnji scenarij" kako bismo zaključili što sa sigurnošću vrijedi. Taj slučaj je ekvivalentan: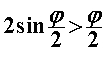 Ova nejednakost nije egzaktno analitički rješiva, već samo numerički te pri tome njeno granično rješenje približno iznosi: 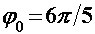 . Zajednički grafički prikaz funkcija s obje strane nejednakosti dan je Slikom 6. Jasno se primjećuje da nejednakost vrijedi za sve vrijednosti . Zajednički grafički prikaz funkcija s obje strane nejednakosti dan je Slikom 6. Jasno se primjećuje da nejednakost vrijedi za sve vrijednosti 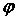 manje od manje od 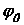 . To znači da dokle god je kut zavoja manji od . To znači da dokle god je kut zavoja manji od 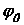 , čak i u slučaju beskonačno tanke staze, "šira" će putanja biti isplativija. , čak i u slučaju beskonačno tanke staze, "šira" će putanja biti isplativija. |
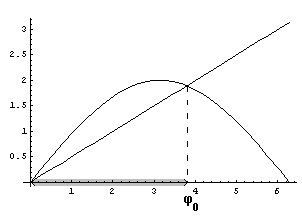 Slika 6 – Grafički prikaz područja vrijednosti promatrane nejednakosti |
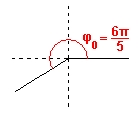 Slika 7 – Raspon kuta φ0 |
Raspon kuta 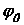 prikazan je na Slici 7 – ako u ozbiljno razmatranje uključimo samo zavoje koji su najviše polukružni, zaključujemo da će u ovakvome modelu prolaska kroz zavoj šira putanja doista uvijek zahtijevati kraće vrijeme. Napomenimo još, argumenta radi, da se podrazumijeva da je u stvarnom slučaju širina staze konačna, stoga će omjer prikazan je na Slici 7 – ako u ozbiljno razmatranje uključimo samo zavoje koji su najviše polukružni, zaključujemo da će u ovakvome modelu prolaska kroz zavoj šira putanja doista uvijek zahtijevati kraće vrijeme. Napomenimo još, argumenta radi, da se podrazumijeva da je u stvarnom slučaju širina staze konačna, stoga će omjer 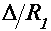 u originalnoj nejednakosti uvijek biti veći od 0 pa će ona vrijediti i za još poprilično širi raspon kuteva od onog minimalnog čija je gornja granica u originalnoj nejednakosti uvijek biti veći od 0 pa će ona vrijediti i za još poprilično širi raspon kuteva od onog minimalnog čija je gornja granica 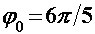 . Fizikalno, vrlo malena vrijednost omjera . Fizikalno, vrlo malena vrijednost omjera 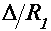 odgovara relativno uskoj stazi vrlo velikoga radijusa zakrivljenosti zavoja. odgovara relativno uskoj stazi vrlo velikoga radijusa zakrivljenosti zavoja. |
 |
Za razliku od prethodnoga modela, u ovome ćemo promatrati što se događa ako na ravnim dijelovima uže putanje usporavamo pri ulasku u zavoj te ubrzavamo pri izlasku. Pri tome će akceleracije biti konstantne i jednakog iznosa. Kroz sâm zavoj i dalje prolazimo konstantnom brzinom 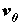 određenom na isti način kao i prije: određenom na isti način kao i prije: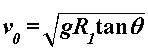 Šira putanja se i dalje sastoji samo od prolaska kroz zavoj te je njeno vrijeme, kao i u Modelu 2: 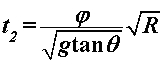 Budući da je su ravni dijelovi na ulasku i izlasku uže putanje jednake duljine 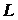 , a duž njih jednakom akceleracijom usporavamo do i ubrzavamo od jedne te iste brzine , a duž njih jednakom akceleracijom usporavamo do i ubrzavamo od jedne te iste brzine 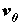 , tada su početna i konačna brzina jednake: , tada su početna i konačna brzina jednake: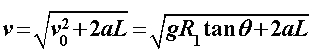 a sukladno tome su jednaka i vremena 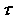 potrebna za prolaz tih komada: potrebna za prolaz tih komada: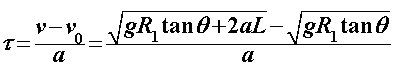 Ukupno vrijeme uže putanje je tada: 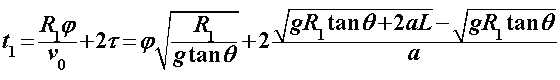 Promotrimo dvije granice. Ako zadamo 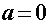 , problem se svodi na Model 2, tj. konstantnu brzinu duž čitave uže putanje – taj slučaj smo već obradili uz zaključak da je u realnim uvjetima šira putanja doista brža od uže. S druge strane, ako uzmemo u obzir beskonačnu vrijednost akceleracije , problem se svodi na Model 2, tj. konstantnu brzinu duž čitave uže putanje – taj slučaj smo već obradili uz zaključak da je u realnim uvjetima šira putanja doista brža od uže. S druge strane, ako uzmemo u obzir beskonačnu vrijednost akceleracije  , tada ravne dijelove uže putanje prolazimo doslovno trenutno pa efektivno za proći ostaje samo zavoj. To je, pak, slučaj iz Modela 1 u kojem smo pokazali da vrijeme prolaska raste s radijusom zavoja. Možemo zaključiti da će za vrijednosti akceleracije do neke maksimalne vremenski isplativija biti šira putanja, a za veće akceleracije uža. Zato moramo izračunati vrijednost te granične akceleracije te iz nje procijeniti isplate li se šire putanje i u ovakvom pristupu prolascima kroz zavoj, te pod kojim uvjetima. , tada ravne dijelove uže putanje prolazimo doslovno trenutno pa efektivno za proći ostaje samo zavoj. To je, pak, slučaj iz Modela 1 u kojem smo pokazali da vrijeme prolaska raste s radijusom zavoja. Možemo zaključiti da će za vrijednosti akceleracije do neke maksimalne vremenski isplativija biti šira putanja, a za veće akceleracije uža. Zato moramo izračunati vrijednost te granične akceleracije te iz nje procijeniti isplate li se šire putanje i u ovakvom pristupu prolascima kroz zavoj, te pod kojim uvjetima.Postupak nalaženja tražene veličine započinjemo iz uvjeta jednakosti vremena za različite putanje: 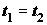 koji je raspisan: koji je raspisan: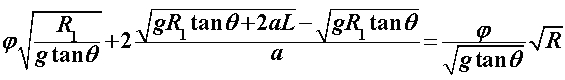 Sređivanjem na prikladniji oblik, jednakost se svodi na: 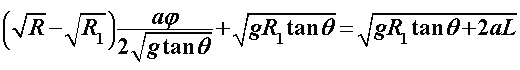 Ovu jednakost kvadriramo nakon čega prelazi u: 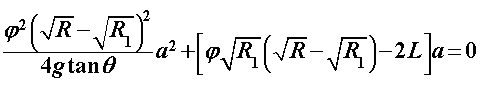 što daje izraz za traženu graničnu akceleraciju: 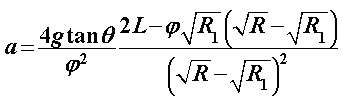 Uz vezu koju smo utvrdili još u Modelu 2: 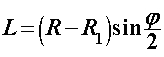 izraz za ključnu akceleraciju 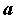 se konačno svodi na oblik: se konačno svodi na oblik: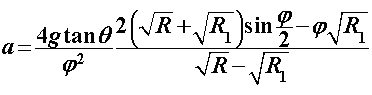 pri čemu je: 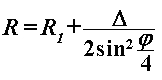 Analizirajmo ponašanje ovog rješenja. Uočavamo da jedino izraz iz brojnika: 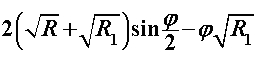 može postati manji od nule, što bi značilo da je za svaku akceleraciju ipak uža putanja isplativija. Zanima nas, dakle, pod kojim uvjetima će ta vrijednost biti pozitivna, a u tu svrhu promatrajmo, kao i u prethodnom modelu, "najcrnji scenarij" koji ćemo simulirati minimiziranjem faktora uz funkciju sinus. To postižemo odabirući 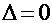 čime vanjski radijus postaje jednak unutarnjem (ponovno, nefizikalan slučaj) te se nejednakost svodi na: čime vanjski radijus postaje jednak unutarnjem (ponovno, nefizikalan slučaj) te se nejednakost svodi na: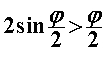 Istom ovom nejednakosti smo se bavili u Modelu 1, stoga ponovno zaključujemo da će uvijek i za sve kuteve koji su manji barem od otprilike 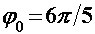 , postojati interval akceleracija za koje će šira putanja još uvijek biti vremenski isplativija. Slijedeće što moramo proučiti je kako izgleda ovisnost granične akceleracije o njenim varijablama te koje će vrijednosti poprimati za pojedine kombinacije tih varijabli. Podsjetimo, šira putanja će biti isplativija za vrijednosti akceleracije manje od granične, stoga nas, zapravo, zanima pod kojim uvjetima šira putanja doista ima prednost pred užom te je li takav pristup prolasku kroz zavoj bolji u, npr., obaranju vremenskih rekorda staze. , postojati interval akceleracija za koje će šira putanja još uvijek biti vremenski isplativija. Slijedeće što moramo proučiti je kako izgleda ovisnost granične akceleracije o njenim varijablama te koje će vrijednosti poprimati za pojedine kombinacije tih varijabli. Podsjetimo, šira putanja će biti isplativija za vrijednosti akceleracije manje od granične, stoga nas, zapravo, zanima pod kojim uvjetima šira putanja doista ima prednost pred užom te je li takav pristup prolasku kroz zavoj bolji u, npr., obaranju vremenskih rekorda staze. |
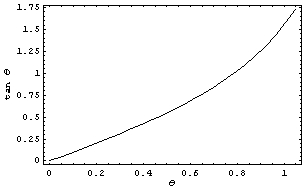 Slika 8 – Funkcija tangens |
Ovisnost o nagibu motocikla 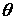 svodi se na funkciju tangens. Za moguće nagibe u obzir ćemo uzeti vrijednosti od 0 pa do ekstremnih π / 3 (60°) – oblik funkcije svodi se na funkciju tangens. Za moguće nagibe u obzir ćemo uzeti vrijednosti od 0 pa do ekstremnih π / 3 (60°) – oblik funkcije 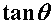 na tome intervalu prikazan je Slikom 8. Primjećujemo da što je nagib veći, to je granična akceleracija viša. na tome intervalu prikazan je Slikom 8. Primjećujemo da što je nagib veći, to je granična akceleracija viša.Za ovisnost o ostalim varijablama bitno je izabrati realistične intervale za svaku od njih. Pri tome ćemo za njihove granice uglavnom odabirati ekstremne vrijednosti da ne bismo izostavili moguće fizikalne situacije. Prema tome, izabiremo slijedeće raspone varijabli (kuteve izražavamo u radijanima, a prostorne skale u metrima): 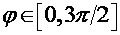 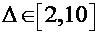 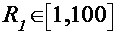 Uz to, u svim slučajevima fiksiramo nagib na istu vrijednost (odabir: 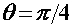 ). ). |
Primjer ovisnosti o unutarnjem radijusu staze i njenoj širini uz fiksni kut zavoja (odabir: 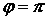 ) dan je na Slici 9. Očito je da u takvom slučaju granična akceleracija s povećanjem radijusa raste, a s povećanjem širine staze pada. To znači da na vrlo širokoj stazi možda neće biti najisplativije izabrati najširu moguću putanju, ali će eventualno još uvijek postojati putanje šire od one najuže, a koje će se i dalje isplatiti. ) dan je na Slici 9. Očito je da u takvom slučaju granična akceleracija s povećanjem radijusa raste, a s povećanjem širine staze pada. To znači da na vrlo širokoj stazi možda neće biti najisplativije izabrati najširu moguću putanju, ali će eventualno još uvijek postojati putanje šire od one najuže, a koje će se i dalje isplatiti.
|
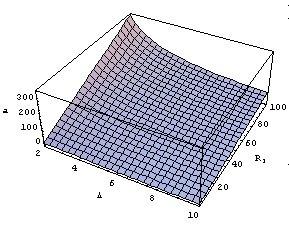 Slika 9 – Ovisnost granične akceleracije o unutarnjem radijusu i širini staze uz fiksni kut zavoja |
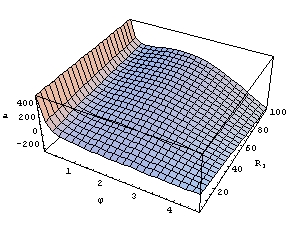 Slika 10 – Ovisnost granične akceleracije o kutu i unutarnjem radijusu zavoja uz fiksnu širinu staze |
Slika 10 prikazuje ovisnost o kutu i unutarnjem radijusu staze uz njenu fiksnu širinu (odabir: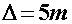 ). U ovom slučaju granična akceleracija opada s porastom i kuta i radijusa, ali na stazi dane širine ponovno vrijedi argument o izboru putanje između najšire i najuže. ). U ovom slučaju granična akceleracija opada s porastom i kuta i radijusa, ali na stazi dane širine ponovno vrijedi argument o izboru putanje između najšire i najuže. |
Na Slici 11 vidi se ovisnost o kutu i širini zavoja uz fiksni radijus (odabir: 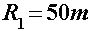 ). Granična akceleracija raste zajedno sa širinom staze, dok je njena ovisnost o kutu malo složenija – uglavnom opada s porastom kuta, dok za vrlo usku stazu u uskom intervalu ima i lagani porast. Negativne vrijednosti se postižu, kao što je već raspravljeno, tek nakon ). Granična akceleracija raste zajedno sa širinom staze, dok je njena ovisnost o kutu malo složenija – uglavnom opada s porastom kuta, dok za vrlo usku stazu u uskom intervalu ima i lagani porast. Negativne vrijednosti se postižu, kao što je već raspravljeno, tek nakon  . . |
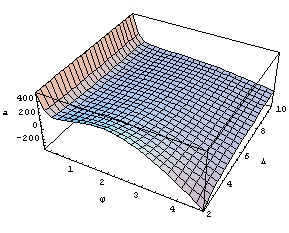 Slika 11 – Ovisnost granične akceleracije o kutu i širini uz fiksni unutarnji radijus zavoja |
U danoj tablici su prikazane vrijednosti granične akceleracije za sve kombinacije izabranih rubnih vrijednosti parametara ovisnosti: |
| θ / rad | φ / rad | R1 / m | Δ / m | a / ms-2 |
|
π / 10 π / 3 |
π / 3 π π / 3 π |
2 100 2 100 2 100 2 100 |
2 10 2 10 2 10 2 10 2 10 2 10 2 10 2 10 |
17.8 14.0 168.6 47.0 5.4 3.4 116.2 25.8 94.7 74.8 898.7 250.4 28.6 18.2 619.6 137.5 |
Današnji motocikli mogu ubrzati od 0 do 100 kmh-1 za otprilike 3 sekunde, što odgovara srednjem ubrzanju od otprilike 9 ms-2. Ako dobiveni rezultat usporedimo s podacima iz tablice, uočavamo da je samo na dva mjesta granična akceleracija niža od one koju je moguće postići. Ti slučajevi odgovaraju malenom kutu nagiba motocikla u polukružnom zavoju vrlo uskoga radijusa – automatski je jasno da situacija odgovara prolasku kroz serpentinu niskom brzinom te je to reprezentativniji slučaj cestovne vožnje, nego na stazi za utrke. Što se tiče ostalih slučajeva, koji više odgovaraju uvjetima na stazi, primjećujemo da su vrijednosti granične akceleracije veće od one koju je uopće moguće postići te ponovno zaključujemo da je šira putanja doista vremenski povoljnija od uže. Uzevši u obzir da je maksimalni mogući nagib motocikla u zavoju izravno povezan s koeficijentom trenja gume i podloge, postaje jasno da, što tehnologija izrade guma postaje naprednija, one time kvalitetnije, a ostvarivanje sve većih nagiba moguće, tim će izbor šire putanje u prolasku zavoja biti još isplativiji. |