sage: var('x y a b c')
(x, y, a, b, c)
U Sageu kao znak jednakosti u jednadžbama stoji ==, jer je uobičajeni znak = rezerviran za pridjeljivanje vrijednosti simbolima odnosno pridjeljivanje imena izrazima. Rješavanje jednadžbi se izvodi funkcijom solve():
sage: sol = solve(2*x^2 - 1 == 0, x); sol
[x == -1/2*sqrt(2), x == 1/2*sqrt(2)]
Valja primijetiti slijedeće:
sage: (x+y).subs(sol[0])
y - 1/2*sqrt(2)
sage: (2*x^2 - 1 == 0).subs(sol[1])
0 == 0
Funkcija solve() može rješavati i sustave jednadžbi, ako se kao argumenti zadaju liste jednadžbi i odgovarajuća lista varijabli:
sage: sol2 = solve([x^2 + y^2 == 1, x - 2*y == 0], [x, y]); sol2
[[x == -2/5*sqrt(5), y == -1/5*sqrt(5)],
[x == 2/5*sqrt(5), y == 1/5*sqrt(5)]]
Da bi dobili numeričke vrijednosti ovih rješenja ne možemo jednostavno primijeniti funkciju numerical_approx() (tj. n()) na ovu listu rješenja, jer n() nije metoda liste (a ni jednadžbe), već samo primitivnijih objekata:
sage: n(sol2)
Traceback (most recent call last):
...
TypeError: unable to coerce to a ComplexNumber: <type 'list'>
Stoga je potrebno nekako primijeniti n() samo na izraze s desne strane gornjih jednadžbi npr.
sage: [(x.subs(sol2[k][0]).n(), y.subs(sol2[k][1]).n()) for k in range(2)]
[(-0.894427190999916, -0.447213595499958), (0.894427190999916,
0.447213595499958)]
Ovo isto možemo izvesti znatno elegantnije [1] koristeći raspakiravanje tupla, te metodu rhs() (right-hand side [2]) za pristup desnoj strani jednadžbe:
sage: [(x.rhs().n(), y.rhs().n()) for x, y in sol2]
[(-0.894427190999916, -0.447213595499958), (0.894427190999916,
0.447213595499958)]
Zadatak 1
Riješite sustav jednadžbi
Koliko ima rješenja?
sage: var('x y') # nužno, jer smo ih gore u petlji redefinirali
(x, y)
sage: # edit here
Ukoliko sustav jednadžbi ima beskonačno rješenja, dobit ćemo rješenje koje uključuje slobodni parametar ili više njih:
sage: solve([x+y == 3, 2*x+2*y == 6],x,y)
[[x == -r1 + 3, y == r1]]
sage: solve([cos(x)*sin(x) == 1/2, x+y == 0],x,y)
[[x == 1/4*pi + pi*z38, y == -1/4*pi - pi*z38]]
Gore je r<broj> neki realni, a z<broj> neki cijeli broj. Ovo radi samo sa sustavom jednadžbi, a ne i s jednom jednadžbom:
sage: solve(sin(x)==0, x)
[x == 0]
Funkcija solve() daje simbolička (analitička) rješenja jednadžbi. Međutim, neka rješenja npr. jednadžbi viših stupnjeva nije moguće analitički zapisati. Npr, za slijedeću jednadžbu solve() nam daje samo jedno trivijalno realno rješenje:
sage: eq = 9*x^6 + 4*x^4 + 3*x^3 + x - 17 == 0
sage: solve(eq, x)
[x == 1, 0 == 9*x^5 + 9*x^4 + 13*x^3 + 16*x^2 + 16*x + 17]
No znamo da ta jednadžba, šestog stupnja, mora imati šest kompleksnih rješenja. Ostalih pet se ne da zapisati drugačije nego kao numeričke (floating point) brojeve. Da bismo dobili ta rješenja koristimo metodu roots, gdje opcijom ring=CC tražimo rješenja u prstenu kompleksnih brojeva:
sage: eq.roots(x, multiplicities=False, ring=CC)
[-1.10301507262981, 1.00000000000000,
-0.491102035999093 - 0.988331495372071*I,
-0.491102035999093 + 0.988331495372071*I,
0.542609572314000 - 1.05431152068711*I,
0.542609572314000 + 1.05431152068711*I]
sage: len(_)
6
Daljnji je problem da je i roots() zapravo analitički rješavač jednadžbi (koristi egzaktne, a ne numeričke metode), a neke jednadžbe se ne mogu analitički egzaktno riješiti, poput onih koje uključuju transcendentalne funkcije.
sage: eq2 = 2 * arctan(x) == x^2
sage: eq2.roots(ring=CC)
Traceback (most recent call last):
...
TypeError: Cannot evaluate symbolic expression to a numeric value.
U tom slučaju moramo pribjeći pravom numeričkom rješavanju, pomoću funkcije find_root(). Mala komplikacija s find_root() je da mu se treba dati interval u kojem traži rješenje i da će pronaći samo jedno. Nakon toga moguće treba tražiti dalje u zadavanjem intervala koji isključuje već pronađena rješenja:
sage: find_root(eq2, 0, 10)
0.0
sage: find_root(eq2, 0.1, 10) # isključujemo 0.0
1.3717743420150883
sage: find_root(eq2, 1.4, 10) # isključujemo i 1.37
Traceback (most recent call last):
...
RuntimeError: f appears to have no zero on the interval
sage: find_root(eq2, -1., 1)
-2.326813826671918e-21
Ovo zadnje rješenje je zapravo 0 jer funkcija find_root() radi numeriku s konačnom preciznošću, koja po defaultu otprilike odgovara preciznosti double precision floating point varijabli u Fortranu ili C-u. Povećavanjem radne preciznosti pomoću opcionalnog argumenta xtol vidimo da se rješenje još više približava nuli:
sage: find_root(eq2, -1., 1, xtol=1e-30)
4.3470345330696587e-32
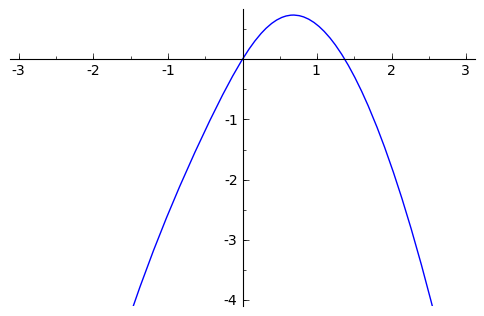
Sada se možemo uvjeriti da su dva pronađena rješenja zaista jedina, i to tako da skiciramo graf funkcije
(čije nultočke su ekvivalentne rješenjima naše jednadžbe) i uočimo da siječe apscisu na samo dva mjesta.
sage: plot(2*arctan(x) - x^2, (x, -3, 3), ymin=-4)
Zadatak 2
Riješite jednadžbu
Zadatak 3
Pronađite numeričku vrijednost nekog kompleksnog rješenja jednadžbe \(\sin x = 2\) i provjerite uvrštavanjem.
Zadatak 4
Riješite nejednadžbu \(x^2 +x - 12 < 0\).
Zadatak 5
Pronađite pozicije lokalnog minimuma te lokalnog maksimuma gama funkcije \(\Gamma (x)\) koji su najbliži točki \(x = 0\)
Zadatak 6
Pronađite pozicije minimuma i maksimuma Besselove funkcije \(J_{1}(x)\) koji su najbliži točki \(x=0\).
Bilješke
| [1] | Općenito, računalni kod koji uključuje duboko indeksiranje višedimenzionalnih lista, poput izraz[0][1] je nepregledan i nepitonican. |
| [2] | Naravno, postoji i lhs(). |