3.4. Crtanje grafova

Glavna Python biblioteka za crtanje grafova je matplotlib. Ona se u Jupyter okruženju može elegantno koristiti tako da se na početku bilježnice pomoću magic komande

%matplotlib inline

zatraži automatsko iscrtavanje slika ispod Jupyter ćelija. Zgodna alternativa je

%matplotlib notebook

koja rezultira time da iscrtane slike postanu interaktivne.

Matplotlib se onda koristi na slijedeći način. Prvo učitavamo potrebne pakete

from scipy import *
import numpy as np
import matplotlib.pyplot as plt
../_images/Plotting-1.png

Za komunikaciju s Matplotlib bibliotekom koristimo modul pyplot (kojeg smo preimenovali u plt) koji omogućuje pristupačno sučelje [1].

Glavna funkcija za crtanje je plt.plot čiji svaki poziv rezultira obično jednom linijom grafa. Ta funkcija kao svoja prva dva argumenta traži liste x i y koordinata točaka koje definiraju liniju grafa. Točke će biti spojene ravnim crtama pa ih treba biti dovoljno da se dobiju glatke krivulje:

xs = np.linspace(0, 2*pi)
plt.plot(xs, sin(xs))
../_images/Plotting-2.png

Svojstva linije kontroliramo opcionalnim argumentima funkcije plot, a za boju i stil postoji i skraćeni oblik:

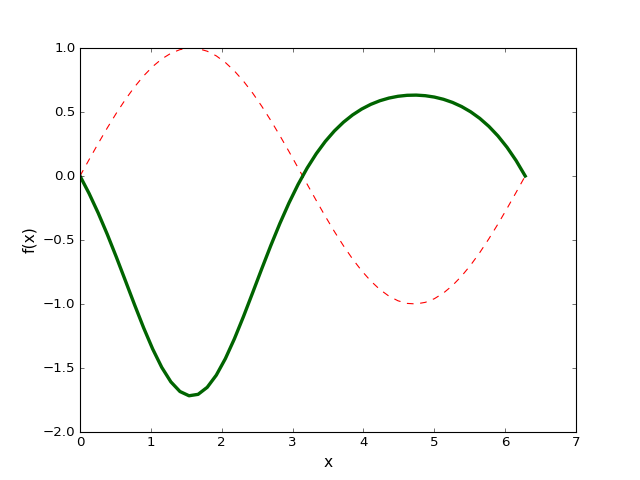
plt.plot(xs, sin(xs), 'r--')
plt.plot(xs, 1-exp(sin(xs)), color='darkgreen',
                        linestyle='-', linewidth='3')
plt.xlabel('x', fontsize=14)
plt.ylabel('f(x)', fontsize=14)
../_images/Plotting-3.png

Matplotlib sam određuje raspon vrijednosti ordinate pogodan za crtanje zadanih funkcija. Ponekad, npr. ukoliko funkcija ima singularitet u području crtanja, to može ispasti loše. No, uvijek možemo i sami specificirati raspon ordinate ylim:

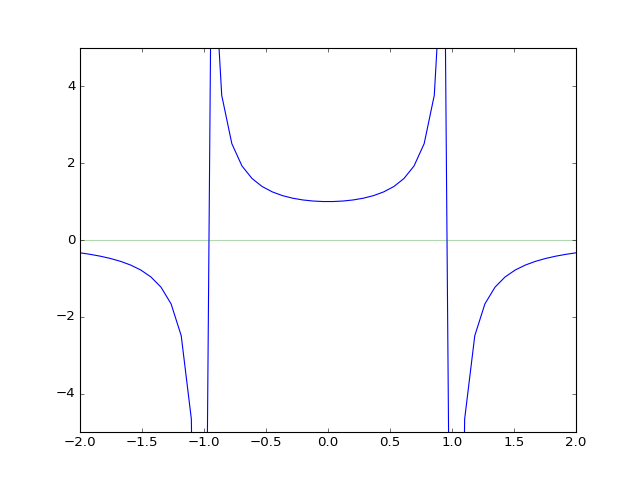
xs = np.linspace(-2, 2)
plt.plot(xs, 1/(1-xs**2))
plt.axhline(0, color='green', alpha=0.3) # transparent line at y=0
fig = plt.ylim(-5, 5)
../_images/Plotting-4.png

Grafove često želimo upotrijebiti i zasebno, npr. u nekom članku ili prezentaciji. Izvoz grafova i drugih objekata postiže se uporabom funkcije plt.savefig(<ime_fajla.ext>). Format grafičke datoteke određen je ekstenzijom. Neke od dopuštenih ekstenzija su .png, .pdf, .ps, .eps, .svg, and .sobj.

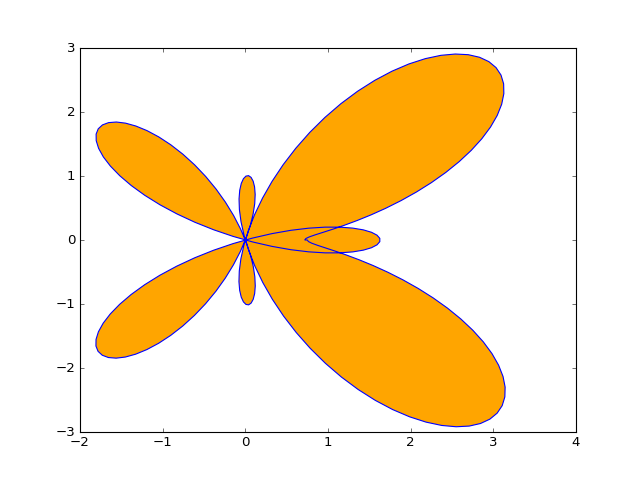
Osim funkcija eksplicitno zadanih u obliku \(y=y(x)\) možemo crtati i funkcije zadane parametarski u obliku \(y=y(t)\), \(x=x(t)\). Npr:

ts = np.linspace(0, 2*pi, 200)
amps = [(exp(cos(t)) - 2*cos(4*t) + sin(t/12)**5) for t in ts]
plt.fill(amps*cos(ts), amps*sin(ts),
         facecolor='orange', edgecolor='blue')
../_images/Plotting-5.png

Za prikaz raznih potencijala i srodnih funkcija, korisna je funkcija plt.contour. Njena tri prva argumenta su tri dvodimenzionalna numpy polja koja po redu odgovaraju vrijednostima \(x\) koordinata točaka u ravnini, \(y\) koordinata te vrijednostima \(f(x, y)\) funkcije koju prikazujemo. Npr. za prikaz funkcije \(f(x,y) = \log(x^2) + y^2\), ta polja priređujemo na slijedeći način

>>> import numpy as np
>>> from scipy import *
>>> xs = np.linspace(1, 5, 60)
>>> ys = np.linspace(-2, 2)
>>> X, Y = np.meshgrid(xs, ys)
>>> Z = log(X**2) + Y**2

>>> xs.shape
(60,)
>>> ys.shape
(50,)
>>> X.shape
(50, 60)
>>> X.shape == Y.shape == Z.shape
True

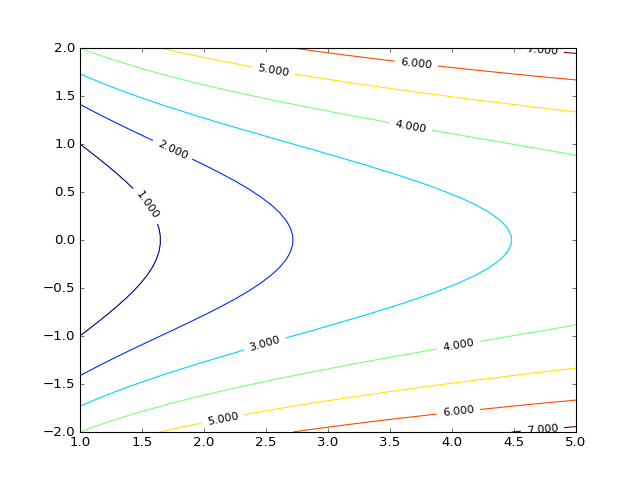
Sada crtamo ekvipotencijalne konture:

CS = plt.contour(X, Y, Z)
fig = plt.clabel(CS, inline=1, fontsize=10, colors='black')
../_images/Plotting-8.png

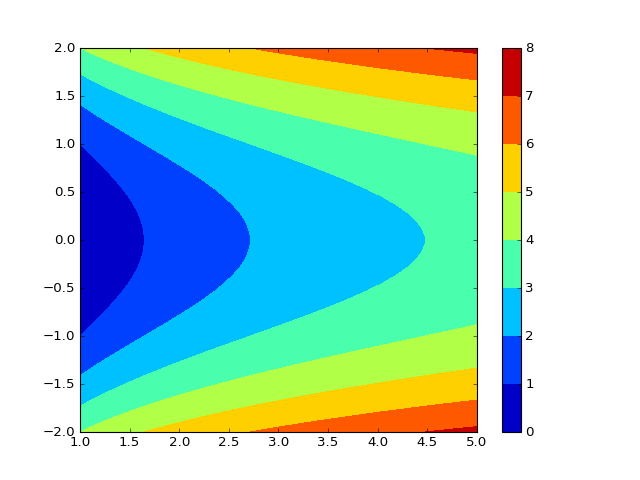
Alternativni prikaz kontura iste ove funkcije:

CS = plt.contourf(X, Y, Z)
plt.colorbar(CS)
../_images/Plotting-9.png

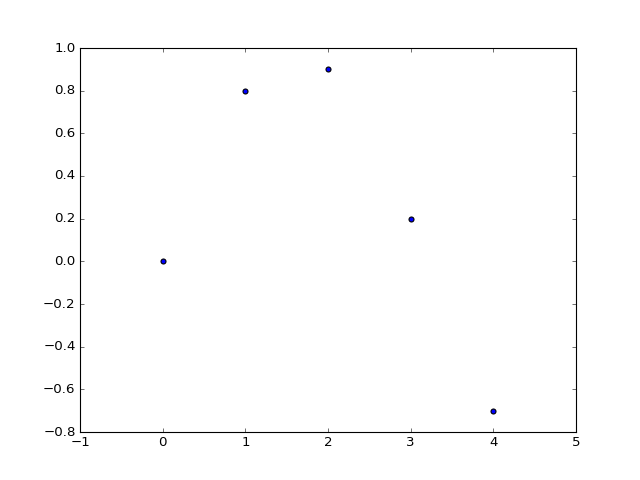
Za crtanje podataka organiziranih u listu parova \([[x_1, y_1], [x_2, y_2], \ldots ]\) rabimo plt.scatter:

data = np.array([[0,0], [1,0.8], [2, 0.9], [3, 0.2],[4, -0.7]])
plt.scatter(data[:,0], data[:,1])
../_images/Plotting-10.png

Gornji primjeri funkcioniraju unutar Jupyter okruženja. U čistom Pythonu potrebno je još dodatno na početku inicijalizirati sliku (za to je dobra funkcija plt.subplots) i na kraju zatražiti njeno iscrtavanje na ekran (plt.show) ili u datoteku (plt.savefig).

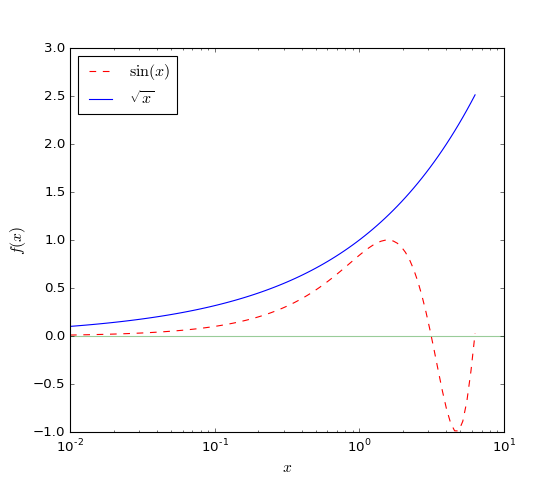
Slijedeći primjer pokazuje graf s logaritamskom osi, legendom i LaTeX oznakama.

xs = np.logspace(-2.0, 0.8, 100)  # granice su log_10(x)
fig, ax = plt.subplots(figsize=[7,6])
ax.plot(xs, sin(xs), color='red', linestyle='--', label='$\sin(x)$')
ax.plot(xs, sqrt(xs), 'b-', label='$\sqrt{x}$')
ax.set_xscale('log')
ax.axhline(0, color='g', linewidth=1, alpha=0.4)
ax.set_xlabel('$x$', fontsize=14)
ax.set_ylabel('$f(x)$', fontsize=14)
ax.legend(loc="upper left")
#fig.show()  # ovo bi trebalo izvan Jupytera
../_images/Plotting-11.png

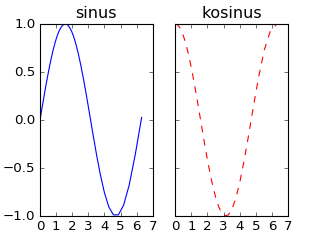
Funkcija plt.subplots stvara dva objekta: sliku (figure) i panel (axis). Složene slike mogu imati više panela, kao u slijedećem primjeru:

fig, (ax1, ax2) = plt.subplots(1, 2, sharey=True, figsize=[4,3])
ax1.plot(xs, sin(xs))
ax1.set_title('sinus')
ax2.plot(xs, cos(xs), color='red', linestyle='--')
ax2.set_title('kosinus')
#fig.show()
../_images/Plotting-12.png

Zadatak 1

Uočite da se funkcija fibBinet(x) iz prošlog odjeljka može izvrijedniti i za vrijednosti argumenta \(x\) koje nisu cjelobrojne. Nacrtajte graf te funkcije za \(-4 < x < 7\) i superponirajte na njega (u drugoj boji) točke koje odgovaraju vrijednostima funkcije za pozitivne cjelobrojne argumente [(1, F_1), (2, F_2), ... (7, F_7)].

Zadatak 2

Koristeći trigonometrijske funkcije nacrtajte kružnicu kao parametarsku krivulju.

Zadatak 3

Nacrtajte 100 slučajno raspoređenih točaka (hint: np.random.rand()), gdje su x i y koordinate tih točaka u intervalu (-1,1), a nacrtane su na dijagramu s x i y osima koje se protežu u intervalu (-2, 2).

Zadatak 4

Nacrtajte kružnicu u kompleksnoj ravnini zadanu kompleksnim brojevima

\[\{ z = \rho e^{i \eta} (1+e^{i\phi}) - 1 \quad | \quad \phi \in [0, 2\pi), \rho = 1.3, \eta = 0.2 \}\]

te krivulju koja se dobije kad se ova kružnica podvrgne transformaciji Žukovskog:

\[z \to w = \frac{1}{2}\left(z+\frac{1}{z}\right)\]

Footnotes

[1]Postoji i modul pylab sa sučeljem sasvim sličnim komercijalnom programu Matlab. Vidi usporedbu raznih Matplotlib sučelja.