>>> from sympy import *
>>> x, y, z, a, b, c = symbols('x, y, z, a, b, c')
4.2. Jednadžbe¶
Simboličko rješavanje jednadžbi se izvodi
funkcijom solveset [1]. Riješimo jednadžbu
>>> sol = solveset(2 * x**2 - 1, x); sol
{-sqrt(2)/2, sqrt(2)/2}
Valja primijetiti slijedeće:
- Jednadžba se postavlja kao izraz kojem se traži nultočka.
- Treba eksplicitno naznačiti po kojoj varijabli se traži rješavanje.
- Pronađena su oba rješenja kvadratne jednadžbe.
- Rezultat je ispisan u obliku skupa. To je najfleksibilniji Sympy objekt koji omogućuje zapis svih vrsta rješenja kakva se mogu pojaviti.
Provjera gornjih rješenja može ići npr ovako:
>>> [2 * x**2 - 1 for x in sol]
[0, 0]
Za linearne sustave jednadžbi koristimo linsolve.
Npr. sustav:
rješavamo ovako:
>>> eqns = [x + 2*y + 3*z - 1, 3*x + y + z + 6, 2*x + 4*y + 9*z - 2]
>>> sol = linsolve(eqns, x, y, z); sol
{(-13/5, 9/5, 0)}
Da bi dobili numeričke vrijednosti ovih rješenja ne možemo jednostavno
primijeniti funkciju N() na ovo rješenje, jer
N() odnosno evalf nije metoda skupa (a ni tupla), već samo primitivnijih objekata:
>>> N(sol)
Traceback (most recent call last):
...
AttributeError: 'Tuple' object has no attribute '_eval_evalf'
Stoga je potrebno nekako primijeniti N() izravno
na brojeve unutar tupla rješenja:
>>> [(N(x), N(y), N(z)) for x,y,z in sol]
[(-2.60000000000000, 1.80000000000000, 0)]
Zadatak 1
Riješite sustav jednadžbi
Koliko ima rješenja?
Evo drugog primjera s beskonačnim skupom rješenja:
init_printing()
solveset(sin(x) - 1, x)
pi
{2*n*pi + -- | n in Integers()}
2
Neka rješenja npr. jednadžbi viših stupnjeva nije moguće analitički zapisati
i solveset daje rezultat u slijedećem obliku:
>>> sol = solveset(9*x**6 + 4*x**4 + 3*x**3 + x - 17, x); sol
{1, CRootOf(9*x**5 + 9*x**4 + 13*x**3 + 16*x**2 + 16*x + 17, 0), CRootOf(9*x**5 + 9*x**4 + 13*x**3 + 16*x**2 + 16*x + 17, 1), CRootOf(9*x**5 + 9*x**4 + 13*x**3 + 16*x**2 + 16*x + 17, 2), CRootOf(9*x**5 + 9*x**4 + 13*x**3 + 16*x**2 + 16*x + 17, 3), CRootOf(9*x**5 + 9*x**4 + 13*x**3 + 16*x**2 + 16*x + 17, 4)}
Vidimo samo jedno realno rješenje i 5 kompleksnih (“Complex root of ...”). Ovo je sad moguće numerički izvrijedniti:
>>> [N(x) for x in sol]
[1.00000000000000, -1.10301507262981, -0.491102035999093 - 0.988331495372071*I, -0.491102035999093 + 0.988331495372071*I, 0.542609572314 - 1.05431152068711*I, 0.542609572314 + 1.05431152068711*I]
Na kraju, neke jednadžbe se uopće ne mogu analitički egzaktno riješiti. Npr.
>>> eq = 2 * atan(y) - y**2
>>> solveset(eq, y)
ConditionSet(y, Eq(-y**2 + 2*atan(y), 0), Complexes((-oo, oo) x (-oo, oo), False))
(Inverzne trigonometrijske funkcije u sympyu (i Pythonovom paketu math)
se zovu atan, asinh itd. dok se u scipy i numpy paketima koriste
arctan, arcsinh itd.)
U gornjem slučaju moramo pribjeći pravom numeričkom rješavanju. Napuštamo
sympy i koristimo scipy.optimize paket i njegovu funkciju root.
Mala komplikacija s root je da je potrebno dati početnu vrijednost
varijable od koje se traži rješenje i da će pronaći samo jedno rješenje.
Također, funkcija čiju nultočku tražimo treba biti
definirana kao Python funkcija.
>>> from scipy import *
>>> from scipy.optimize import root
>>> def fun(y):
... return 2 * arctan(y) - y**2
>>> sol = root(fun, 0); sol
fjac: array([[-1.]])
fun: array([ 0.])
message: 'The solution converged.'
nfev: 3
qtf: array([ 0.])
r: array([-1.99999999])
status: 1
success: True
x: array([ 0.])
Vidimo da je rješenje koje daje root složeni objekt, a samoj
vrijednosti nultočke pristupamo putem atributa x (koji se zove
x bez obzira na to kako se zove varijabla funkcije, u našem
slučaju y!).
Eventualno drugo rješenje treba tražiti dalje zadavanjem drugih početnih vrijednosti.
>>> sol = root(fun, 1); sol.x[0]
1.371774342015089
Nastavljamo dalje ...
>>> sol = root(fun, 10); sol.x[0]
1.371774342015089
>>> sol = root(fun, -10); sol.x[0]
0.0
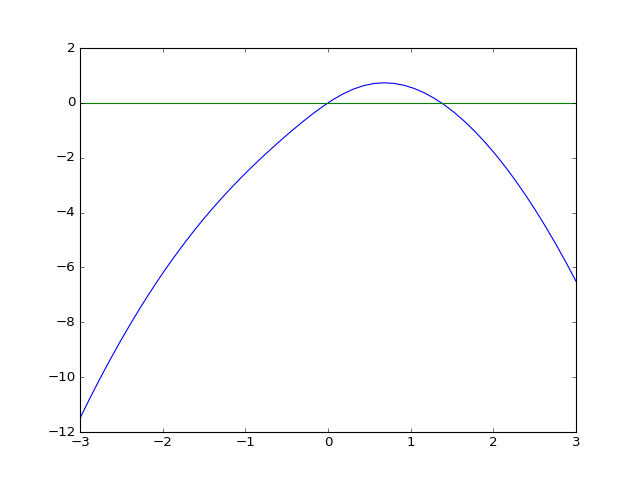
Sada se možemo uvjeriti da su dva pronađena rješenja zaista jedina, i to tako da skiciramo graf funkcije i uočimo da siječe apscisu na samo dva mjesta.
>>> from scipy import *
>>> from scipy.optimize import root
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def fun(y):
... return 2 * arctan(y) - y**2
>>> xs = np.linspace(-3, 3)
>>> fig = plt.plot(xs, fun(xs))
>>> fig = plt.axhline(0, color='green')
Inače, kad nam treba jednostavna “funkcija za jednokratnu upotrebu”, poput
funkcije fun gore, možemo koristiti tzv. lambda-funkciju
>>> sol = root(lambda x: 2 * arctan(x) - x**2, 1); sol.x[0]
1.371774342015089
Također, za brzu pretvorbu simboličkih izraza u Python funkcije, korisna
je funkcija lambdify. Tako smo gore, prilikom numeričkog rješavanja
jednadžbe, umjesto definiranja nove funkcije mogli “lambdificirati”
već definirani simbolički izraz.
>>> root(lambdify(y, eq), 1).x[0]
1.371774342015089
Ovo omogućuje i crtanje simboličkog izraza matplotlibom (opcija
numpy dolje omogućuje lambda funkciji da se distribura
po numpy polju):
plt.plot(xs, lambdify(y, eq, 'numpy')(xs))
fig = plt.axhline(0, color='green')
No, za jednostavne skice simbličkih izraza možemo koristiti
i sympy funkciju plot:
plot(eq, (y, -3, 3))
Za usporedbu raznih pristupa pretvorbi simboličkih izraza u numeričke, vidi tablicu na kraju ove stranice.
Zadatak 2
Riješite jednadžbu
Zadatak 3
Pronađite pozicije lokalnog minimuma te lokalnog maksimuma gama funkcije \(\Gamma (x)\) koji su najbliži točki \(x = 0\)
>>> from scipy.special import gamma
>>> from scipy.optimize import minimize
Zadatak 4
Pronađite pozicije lokalnih minimuma i maksimuma Besselove funkcije \(J_{1}(x)\) koji su najbliži točki \(x=0\).
>>> from scipy.special import j1
>>> from scipy.optimize import minimize
Zadatak 5
Krivulje
za svaki \(\alpha\) prolaze kroz istu točku \((x_0, y_0)\). (U to se možete i grafički uvjeriti.) Definirajte funkciju \(y(x, \alpha)\), zatim rješavanjem sustava jednadžbi odredite tu točku i na kraju ispišite broj \(x_0 + y_0\).
Bilješke
| [1] | Postoji i stara funkcija solve koja je inferiorna ovoj, osim za nelinearne susustave jednadžbi. Vidi ovdje. |