4.5. Diferencijalne jednadžbe

4.5.1. Simboličko rješavanje

Python sympy funkcija koja traži analitička rješenja običnih diferencijalnih jednadžbi je desolve(). Riješimo pomoću nje jednadžbu gušenog harmoničkog oscilatora

\[\frac{d^2 y}{d t^2} + 2 \frac{dy}{dt} + 4y = 0 \,.\]

Prilikom definiranja diferencijalne jednadžbe treba eksplicitno deklarirati simboličku nezavisnu varijablu (obično je to vrijeme t) i nepoznatu simboličku funkciju (ovdje je to y(t)), pomoću opcije funkcije symbols:

>>> from sympy import *
>>> t = symbols('t')
>>> y = symbols('y', cls=Function)

>>> gsol = dsolve(y(t).diff(t, t) + 2*y(t).diff(t) + 4*y(t), y(t)); gsol
Eq(y(t), (C1*sin(sqrt(3)*t) + C2*cos(sqrt(3)*t))*exp(-t))

Napomene:

1. Kao što je kod običnih jednadžbi trebalo eksplicirati po kojoj varijabli se traži rješenje, tako se kod diferencijalnih specificira po kojoj funkciji se traži rješenje
2. Rješenje je izraženo kao sympy jednadžba (objekt tipa Eq) i za pristup samoj funkciji možemo koristiti metodu rhs
3. Rješenje je općenito tj. uključuje nepoznate konstante ( \(C_1\) i \(C_2\)) koje treba odrediti iz početnih uvjeta. To je moguće npr. na slijedeći način

>>> C1, C2 = symbols('C1, C2')
>>> consts = linsolve([gsol.rhs.subs(t,0) - 1, gsol.rhs.diff(t).subs(t, 0) -1], C1, C2); consts
{(2*sqrt(3)/3, 1)}

Sad možemo ove konstante uvrstiti u rješenje. Prvo ćemo tupl koji je element jednočlanog skupa rješenja pretvoriti u rječnik:

>>> dics = [{C1:c1, C2:c2} for c1, c2 in consts]; dics
[{C2: 1, C1: 2*sqrt(3)/3}]

>>> sol = gsol.rhs.subs(dics[0]); sol
(2*sqrt(3)*sin(sqrt(3)*t)/3 + cos(sqrt(3)*t))*exp(-t)

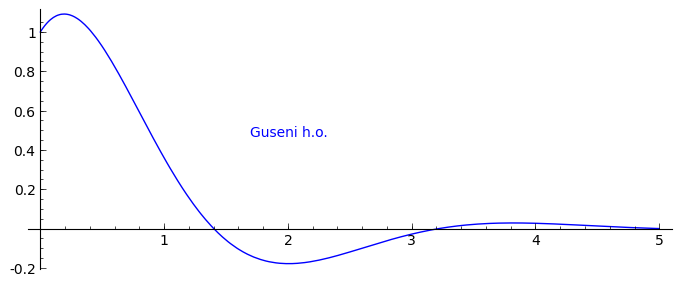
To je sad konkretno rješenje koje možemo nacrtati npr kao

>>> plot(sol, (t, 0, 10))

Zadatak 1

Riješite simbolički diferencijalnu jednadžbu

\[\frac{dy}{dt} - y^2 - 1 = 0 \;,\]

uz početni uvjet \(y(0)=1/2\), provjerite rješenje uvrštavanjem, te ga nacrtajte za t u rasponu \(0<t<1\).

4.5.2. Numeričko rješavanje

Neke jednadžbe se ne mogu riješiti analitički, pa moramo pribjeći numeričkom integriranju. Za to ćemo koristiti funkciju odeint iz paketa scipy.integrate.

>>> from scipy.integrate import odeint
>>> import matplotlib.pyplot as plt
>>> import numpy as np

Kao prvi primjer integrirati ćemo jednadžbu iz gornjeg zadatka. Za odeint tu jednadžbu treba transformirati u oblik

\[\frac{dy}{dt} = f(y,t)\]

i korisnik treba definirati Python funkciju koja odgovara desnoj strani ove jednadžbe.

U našem slučaju je \(f(y, t) = y^2 + 1\) pa stoga imamo

>>> def func(y, t):
...     return y**2 + 1

Funkciju odeint treba pozvati s ovom funkcijom kao prvim argumentom, početnom vrijednošću \(y(0)\) kao drugim argumentom i listom vremenskih točaka za koje želimo odrediti položaj sustava kao trećim argumentom:

>>> y0 = 0.5
>>> ts = np.linspace(0, 1)
>>> ts.shape
(50,)

Funkcija odeint vraća listu položaja u traženim vremenskim točkama:

>>> ys = odeint(func, y0, ts)
>>> ys.shape
(50, 1)

>>> print("\n{:8s}  {:8s}".format('vrijeme', 'položaj'))
>>> print(18*'-')
>>> for t,y in zip(ts[:5], ys[:5, 0]):
...     print("{:8f}  {:8f}".format(t, y))
>>> print("{:8s}  {:8s}".format(' (...)  ', ' (...)  '))

 vrijeme  položaj
------------------
0.000000  0.500000
0.020408  0.525777
0.040816  0.552113
0.061224  0.579049
0.081633  0.606630
 (...)     (...)

plt.plot(ts, ys)

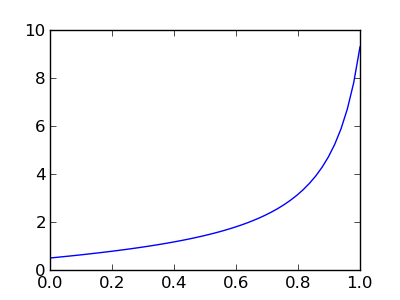
Kao slijedeći primjer proučiti ćemo tzv. van der Polovu jednadžbu, koja je drugog reda:

\[\frac{d^2 x}{d t^2} - (1-x^2) \frac{dx}{dt} + x = 0 \,.\]

Jednadžbe višeg reda se za numeričku analizu treba prirediti tako da se svaka pretvori u sustav od dvije jednadžbe prvog reda, što se izvodi uvođenjem nove funkcije \(y(t)=dx/dt\) uz pomoć koje gornju jednadžbu možemo pretvoriti u ekvivalentni sustav

\[\frac{dx}{dt} = y\]

\[\frac{dy}{dt} = (1-x^2)y -x\]

Taj sustav sad treba zapisati u vektorskom obliku tako da poprimi strukturu

\[\frac{dy_k}{dt} = f_k(\vec{y}, t)\,, \qquad k=1,2\]

gdje je dvokomponentni vektor \(\vec{y} = (x, y)\equiv\) [y[0], y[1]]. Sada funkcija koju priređujemo za odeint opet odgovara desnoj strani ove jednadžbe i mora kao rezultat vratiti dvokomponentni vektor \(\vec{f} = (f_1, f_2)\)

>>> def func(y, t):
...     return [y[1], (1 - y[0]**2)*y[1] - y[0]]

Početni uvjet je isto vektor \((x(0), y(0))\), a i rezultat će biti NumPy polje oblika (broj vremenskih točaka) x (broj nepoznatih funkcija).

>>> ts = np.linspace(0,15,150)
>>> y0 = [1., 1.]
>>> ys = odeint(func, y0, ts)
>>> ys.shape
(150, 2)

>>> fig, ax = plt.subplots(figsize=[7,3])
>>> ax.plot(ts, ys[:,0], label='x(t)')
>>> ax.plot(ts, ys[:,1], label='y(t)')
>>> ax.legend()

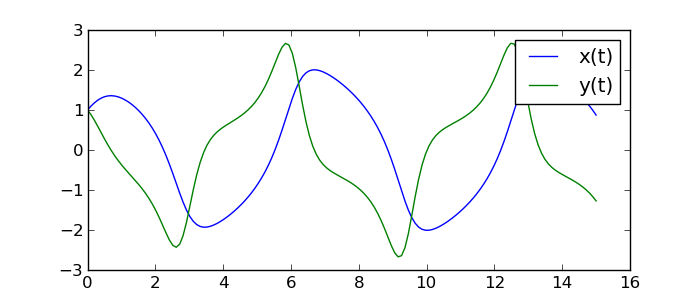
Zadatak 2

Nacrtajte graf brzine gornjeg rješenja Van der Polove jednadžbe \(y(t)=dx(t)/dt\), ali ne u ovisnosti o vremenu \(t\), već o položaju \(x(t)\) (tzv. fazni dijagram).

Zadatak 3

Riješite numerički diferencijalnu jednadžbu gušenog harmoničkog oscilatora. Nacrtajte funkcije y(t) i x(t), te, na posebnom grafu, fazni dijagram y(x).